Combining Multiple Biometrics
John Daugman, The Computer Laboratory,
Cambridge University
Overview
This short note investigates the consequences of combining two or more
biometric tests of identity into an enhanced "layered" test. There is a
common and intuitive assumption that the combination of different tests
must improve performance, because "surely more information is better
than less information." On the other hand, a different intuition suggests
that if a strong test is combined with a weaker test, the resulting
decision environment is in a sense averaged, and the combined performance
will lie somewhere between that of the two tests conducted individually
(and hence will be degraded from the performance that would be
obtained by relying solely on the stronger test).
There is truth in both intuitions. The key to resolving the apparent
paradox is that when two tests are combined, one of the resulting
error rates (False Accept or False Reject rate)
becomes better than that of the stronger of the two tests,
while the other error rate becomes worse even than that of the weaker of the
tests. If the two biometric tests differ significantly in their power,
and each operates at its own cross-over point,
then combining them gives significantly worse performance than
relying solely on the stronger biometric.
Notation
Two hypothetical and independent biometric tests will be considered here, named
1 and 2. For example, 1 might be voice-based
verification, and 2 might be fingerprint verification.
Each biometric test is characterized by
its own pair of error rates at a given operating point, which I will
denote as the error probabilities P1(FA), P1(FR), P2(FA),
and P2(FR):
P1(FA) = probability of a False Accept using Biometric 1
alone.
P1(FR) = probability of a False Reject using Biometric 1
alone.
P2(FA) = probability of a False Accept using Biometric 2
alone.
P2(FR) = probability of a False Reject using Biometric 2
alone.
There are two possible ways to combine the outcomes of the two biometric tests
when forming the conjoint ("enhanced") decision: the Subject may be required
to pass both of the biometric tests, or he may be accepted if he can
pass at least one of the two tests. These two cases define the
disjunctive and conjunctive rules:
Rule A: Disjunction ("OR" Rule) - Accept if either
test 1 or test 2 is passed.
Rule B: Conjunction ("AND" Rule) - Accept only if both
tests 1 and 2 are passed.
We can now calculate False Accept and False Reject error rates of the
combined biometric, both for disjunctive (Rule A) and conjunctive
(Rule B) combinations of the two tests.
These new error probabilities will
be denoted: PA(FA), PA(FR), PB(FA), and PB(FR).
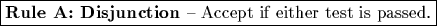
If Rule A (the "OR" Rule) is used
to combine the two tests 1 and 2, a False Reject can only occur
if both tests 1 and 2 produce a False Reject. Thus the combined
probability of a False Reject, PA(FR), is the product of its two
probabilities for the individual tests:
PA(FR) = P1(FR)P2(FR)
(clearly a lower probability than for either test alone). But the
probability of a False Accept when using this Rule, which can be expressed
as the complement of the probability that neither test 1 nor 2
produces a False Accept, is higher than
it is for either test alone:
PA(FA) = 1-[1-P1(FA)][1-P2(FA)]
= P1(FA) + P2(FA) - P1(FA)P2(FA)

If Rule B (the "AND" Rule) is used
to combine the two tests 1 and 2, a False Accept can only occur
if both tests 1 and 2 produce a False Accept. Thus the combined
probability of a False Accept, PB(FA), is the product of its two
probabilities for the individual tests:
PB(FA) = P1(FA)P2(FA)
(clearly a lower probability than for either test alone). But the
probability of a False Reject when using this Rule, which can be expressed
as the complement of the probability that neither test 1 nor 2
produces a False Reject, is higher than
it is for either test alone:
PB(FR) = 1-[1-P1(FR)][1-P2
(FR)]
= P1(FR) + P2(FR) - P1(FR)P2(FR)
Example:
Combination of two hypothetical biometric tests, one stronger than the other:
Suppose weak Biometric 1 operates with both of its error rates
equal to 1 in 100, and
suppose stronger Biometric 2 operates with both of its error rates
equal to 1 in 1,000. Thus if
100,000 verification tests are conducted with impostors and another 100,000
verification tests are conducted with authentics, Biometric 1 would
make a total of 2,000
errors, whereas Biometric 2 would make a total of only 200 errors.
But what happens if the two biometrics are combined
to make an "enhanced" test?
If the "OR" Rule is followed in the same batch of tests,
the combined biometric would make 1,099 False Accepts and 1 False Reject,
for a total of 1,100 errors.
If instead the "AND" Rule is followed,
the combined biometric would make 1,099 False Rejects and 1 False Accept,
thus again producing a total of 1,100 errors. Either method
of combining the two biometric tests produces 5.5 times more errors
than if the stronger of the two tests had been used alone.
Conclusion: A strong biometric is better alone
than in combination
with a weaker one...
when both are operating at their cross-over points. To reap benefits
from decision combination, the equations above show that the operating point of
the weaker biometric must be shifted to satisfy the following criteria:
If the "OR" Rule is to be used, the False Accept rate of the weaker test
must be made smaller than twice the cross-over error rate of the stronger test.
If the "AND" Rule is to be used, the False Reject rate of the weaker test
must be made smaller than twice the cross-over error rate of the stronger test.
If two biometric tests of equal power are combined -- for example encoding
both eyes' iris patterns, or two of a person's fingerprints -- then the
appropriate shift in operating threshold (whether for the "AND" rule or the "OR" rule)
will enhance performance and reduce the net equal-error rate. In the particular case
of the author's algorithms for iris recognition, for example, when using a two-eyed
"AND" rule the decision criterion may be put as high as 0.38 Hamming Distance
(allowing as many as 38% of the bits to disagree while still declaring a match,
thus significantly reducing False Reject Rate while keeping the False Accept
probability still infinitesimally small). Decision Environment dual histogram
distributions for single eye comparisons are illustrated
here.
This short note has considered only a case of decision-level fusion, or layering.
Other methods of combining biometrics include sensor fusion
(combining feature data before applying any decision rule), or combining
similarity scores before applying any decision rule.
Important papers in this space include the following:
- Chapter 7, "Multimodal Biometric Systems," in Handbook of Fingerprint
Recognition by Maltoni, Maio, Jain, and Prabhakar (2003), Springer-Verlag
(ISBN 0-387-95431-7). See especially
pp 239-243, Figure 7.2 and Table 7.1 (p 240 and 243).
- Nigel Sedgwick's paper on multi-modal biometric combination, November 2003:
http://www.camalg.co.uk/s03017_pr0/s03017_pr0.pdf
-
Kittler, Li, Matas, and Ramos-Sanchez (1997) "Combining evidence in multimodal
personal identity recognition systems." Int'l. Conf. on Audio- and Video-Based
Biometric Person Authentication.
- Jain, Duin, and Mao (2000) "Statistical pattern recognition: A review."
IEEE Transactions on Pattern Analysis and Machine Intelligence,
vol 22 (1), pp 4 - 37.
- Kittler, Hatef, Duin, and Matas (1998) "On combining classifiers."
IEEE Transactions on Pattern Analysis and Machine Intelligence,
vol 20, pp 226 - 239.
- Roli, Kittler, Fumera, and Muntoni (2004) "An experimental comparison of
classifier fusion rules for multimodal personal identity verification systems."
Available here.
Back to Main Page.