A synchronous FSM is a low-level representation of part of a hardware design and the amount of transformation possible is limited compared with what can be done when only some aspect of it needs to be preserved.
In this monograph we review various forms and techniques for re-timing and re-pipelining synchronous logic.
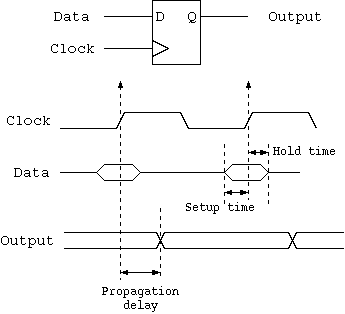
The input data for a D-type flip-flop must be stable before the aperture opens, otherwise the flip-flop may not work properly (overclocking). The aperture is defined by the set-up and hold times in the flip-flop data sheet.

Some flip-flops have lower clock-to-Q propagation time than hold time. These are not often found in modern technology since a shift-register-like structure is illegal. The classic papers regarding retiming assume the general case and need to guard against hold time violations. We here assume that hold time is less than clock-to-Q time and can always be ignored.
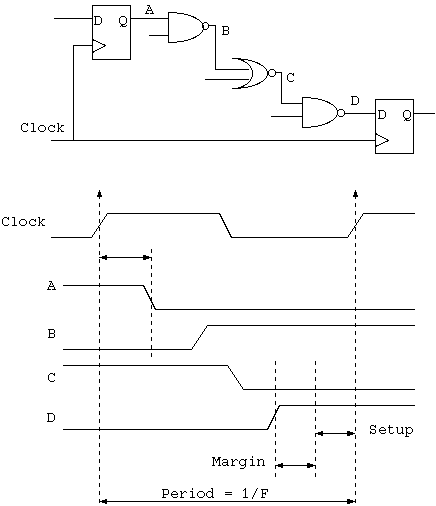
The maximum clock frequency of a synchronous clock domain is set by its critical path. This is the longest path of combinational logic and it must have settled before the setup time of any flip-flop starts.
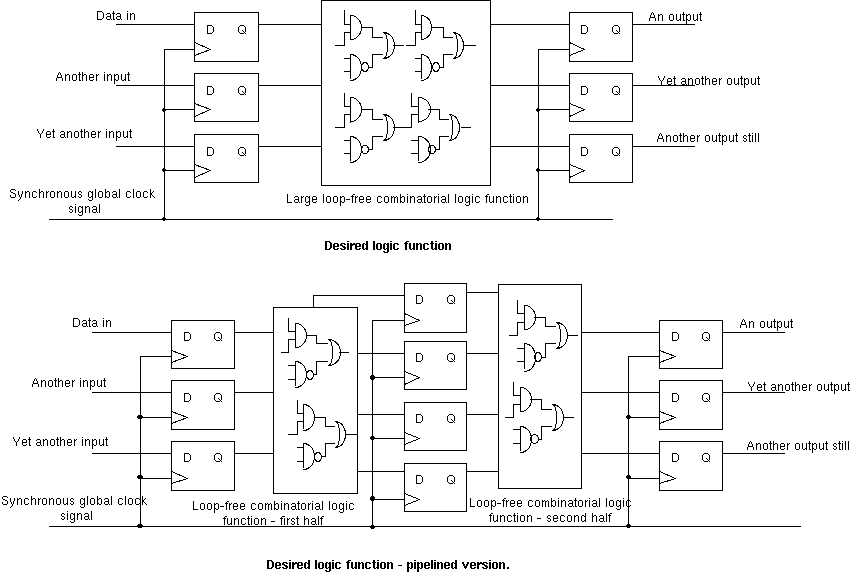
The hardware equivalent of a software basic block is a loop-free combinational circuit with some number of registers but no feedback from one register to an earlier one. Such a design presents no problem to re-pipeline to achieve a higher clock frequency. We shall always assume that the end user can tolerate the data arriving some number of cycles later.
Where there is no feedback from a later to an earlier register, we say the design has no sequential loops or has no sequential feedback.
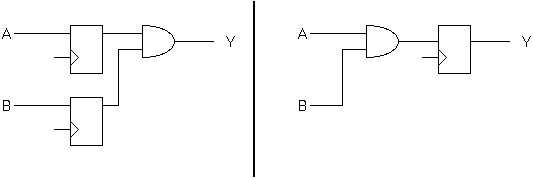
Flip-flop migration alters state encoding. Migration may be manually turned on or off during logic synthesis by typical RTL compiler tools. It exchanges delay in one path for delay in another. The aim is to achieve balanced delays along all paths. A sequence of such transformations can lead to a shorter critical path overall.
We only consider D-type flip-flops in this work and all are assumed to be in the same synchronous clock domain. We do not consider multi-cycle paths.
Gray coding and one-hot encoding transforms are often applied locally to a part of the state vector. A set of D-types is replaced with another set of a similar or larger size with different encoding. There is an injection of the old state encoding into the new state space. The typical benefit of this is that logic which reads this part of the state vector becomes more simple.
In general we need to distinguish between transformations where the original state can be reconstructed with a stateless (combinational) function and those that require state (typically just broad-side shift registers) to reconstruct. Gray and one-hot transformations required stateless reconstruction functions.
Also note that we are typically only interested in reconstructing part of the full state. We are interested in the observable output which we shall later phrase as the support of the output labelling function.
Synchronous FSMs (finite-state machines), with no input and output, are an important class of problem. We shall later speak of how to add input and output. The input and output ports will need handshaking since we will be stuttering. A stuttering equivalence between two designs is where they achieve the same function or behaviour, but take a different number of clock cycles to achieve it and where they may freely pause or skip clock cycles where this does not affect the function or behaviour.
Where an FSM without input or output is transformed, there often needs to be an accompanying transformation on the initial and final states. The initial state is what is loaded into the FSM before the first clock cycle. It might contain data arguments for a computation. The final state needs to be flagged by a separately-defined observer function. This will typically spot a 'halt' pattern in some bit or bits of state and then yield the 'result' from another part of the state. A variant is that the machine issues a sequence of results over time defined with a similar observer function.
The transformations on initial state and observer function are normally fairly easily to run in shotgun with the transformations on the main FSM, so we shall only return to them when we consider FSMs with handshaked input and output.
The classic work on retiming FSM was "Leiserson C., Saxe B., “Optimizing Synchronous Systems”, Journal of VLSI and Computers Systems, pp. 41-67, 1983".
There are two standard transformation rules that can be classically applied: double and shift.
Sometimes area is not a concern and a large amount of logic replication is allowable if it results in a shorter critical path. We shall assume this as the general case except for certain structures that we are not allowed to modify and would desire not to replicate.
One class of interesting components consists of a synchronous instruction ROM for a microcontroller or the synchronous instruction cache of a processor. We can safely assume that updates never happen or can be ignored. We can then treat them as expensive combinational logic functions that we cannot transform during re-timing and that are permanently hardwired to their output register.
Similarly, some pipelined, stateless functions, such as ALUs and other functional units (FUs), cannot be transformed since they are hardened macros or leaf components. Generally we can replicate these. The overall figure of merit for a design may or my not depend on the degree of replication.
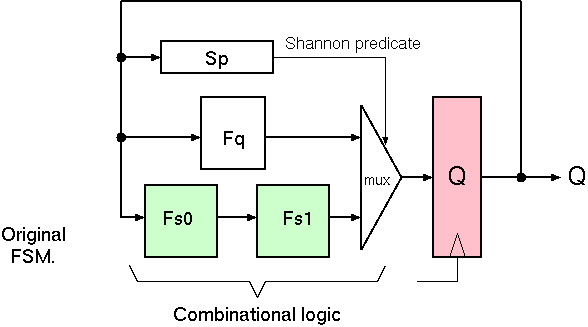
Without loss of generality, any combinational function can represented as a mux of two combinational functions where the mux predicate is typically one of the input nets but can also be a third function of the inputs. This is called the Shannon Decomposition of a function.
Often, the NSF (next-state function) of a canonical FSM can be Shannon decomposed into a fast path and a slow path.
Given this factorisation of the NSF, we make a stuttering equivalence by putting a pipeline stage in the slow path and de-asserting the clock enable input to the main state vector while the slow path is in operation. A signal is also forwarded to the output labelling functions to indicate the stutter, so that a wrongful repetition of an observable output is suppressed.
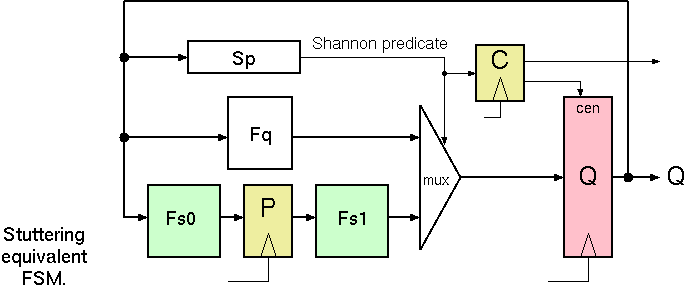
Shannon-based Pipeline Transform Applied.
If the NSF and the observer functions are expressed as BDDs (binary decision designs), then bisimulation transformations can be applied. These preserve observable behaviour.

Core Reduction Implementation (from Greaves 07).
Greaves 07 reduced hardware complexity with such transformations. Links: BDD: L1 MEH: L2
However, a follow-on transformation to selectively increase state and clock frequency is ongoing work.
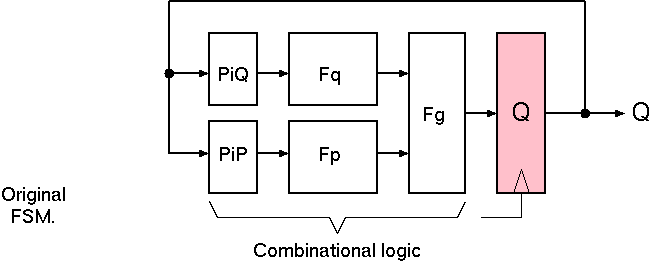
Original FSM: NSF Factorised but not pipelined.
Without loss of generality, a canonical FSM with state Q can have its NSF (next-state function) partitioned into two separate functions Fp and Fq as shown. They are recombined with a third function Fg. Moreover, Fp and Fq are chosen such that they mostly depend on disjoint regions of the state vector Q. This is illustrated with the projection functions Pi P and Pi Q which select the supporting nets from Q.
Given this factorisation of the NSF, we perform the pipeline projection by computing Fp the clock cycle before Fq. This will be done using the
extra register P. The redrawn diagram shows Fp still computed at the same time as Fq, but a new migration zone that contains the identity function is also shown. All of
Fp can be migrated to this zone. In addition, the zone can access the output of the Pipeline register which will be useful (see section X of the paper).
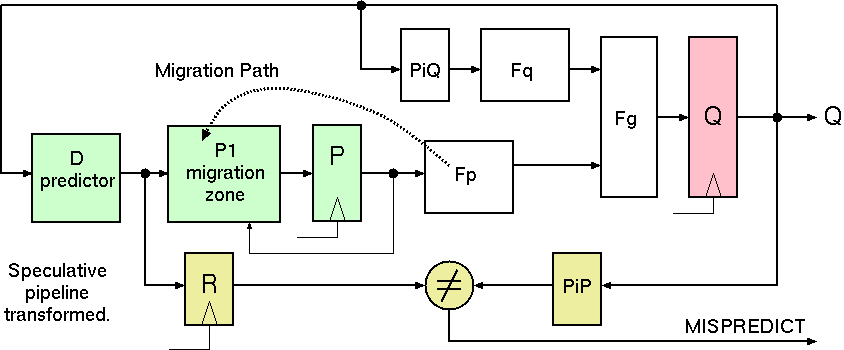
Speculative Pipeline Transform Applied.
The input to the migration zone is the output of a predictor of what Pi P will deliver in the next clock cycle. This prediction may be wrong, in which case a comparison with the actual Pi P output during the next clock cycle will be sufficient to flag the output Q as invalid to observing logic. Not shown in the diagram is the additional step to correct or reload Q from a saved copy, but this is included in the algebraic formalism in section X of the paper and shown to be correct.
The textbook pipelined CPU design can be generated from a non-pipelined equivalent using speculation that the current instruction does not represent a taken branch. In essence, if it turns out to be a taken branch, the design stutters and state is reset to previous or corrected accordingly.
In the general case of the speculative stuttering transform, we partition the state vector into two, as per Leiserson, but instead of providing an earlier version of the bottom-to-top flow we provide a speculative value for it. A clock cycle later we find out the true value and then need to handle a mis-match.
Heuristic search or manual expression is needed to locate good speculation predicates. Profile-directed feedback is essential since the duty cycle of a net or expression cannot be statically determined for FSMs that approach Turing completeness in scale or where only a limited set of starting conditions is of interest.
... temporaly floating I/O ... to be finished ...
...
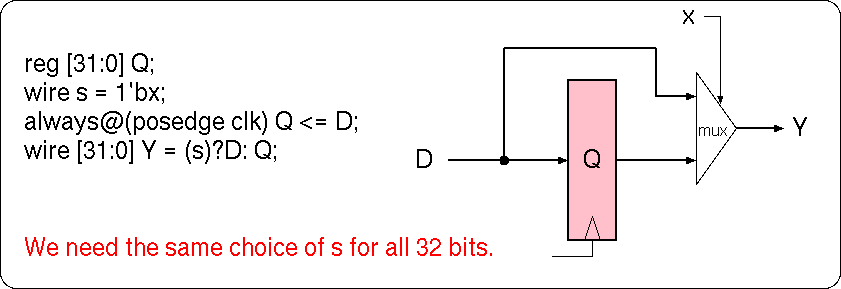
For combinational logic, we are used to logic synthesis tools generating minimal designs based on free choice in dont-care conditions.
For sequential logic, layout-aware back end tools should be able to make similar decisions for sequential paths.
The non-deterministic temporal mux design pattern could work as outlined in this figure. As with a model checker, we have not specified the value on the disconnected input. But unlike model checkers, current logic synthesis tools will freely choose independent values for the mux input for each of the 32 bit lanes. This is not what the designer wanted!
The output from a higher-level synthesis tool, (eg. a simple Bluespec compiler Toy BSVC) embodies arbitrary decisions made by that tool. The tool may have used heuristics to attempt a good design, but perhaps the design can be further improved by re-timing. For Bluespec, there was freedom about rule schedulling. Also, much of the data was tagged with valid bits, but the generated RTL may not include any or sufficient don't cares for invalid data (dead values) to be safely ignored. Back end improvements are thus limited by lack of information.
A typical example where post-processing is needed is for a simple syntax-directed compiler that generates many adders in its output. Either it registers on a regular basis (eg. every 16 bits of partial sum) or it does not register at all. Either way, it generates a large circuit with periodicly repeating structure. No localised decision or policy can generate the best design globally. The optimum design point has different behaviour in different cycles of the repeated structure, such as registering every 5th partial sum.
The higher ... to be finished ... Live Data Provenance Backward Analysis ...
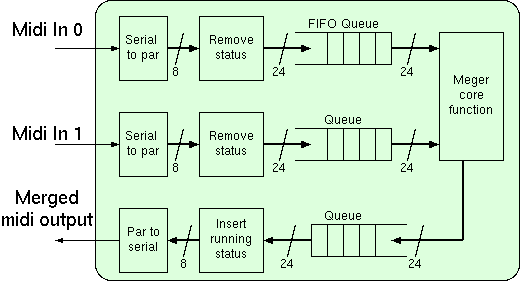
Midi Merge Unit Block Diagram.
... to be finished ...
(C) DJ Greaves 2000-2019.