A Taxonomy of Diagram Taxonomies

Alan F. Blackwell and Yuri Engelhardt

In Proceedings of Thinking with Diagrams 98: Is there a science of diagrams?, pp. 60-70.

Abstract

A large number of taxonomic approaches have been proposed for the study of diagrammatic representations. We have reviewed existing taxonomic systems as well as current research questions in this multi-disciplinary community. Based on this review, we propose a set of taxonomic dimensions that can be used for analysing and comparing existing taxonomic systems, and for assessing their relevance to specific research questions. The proposed framework also enables a comparative positioning of the various research endeavours in this multi-disciplinary field.

Introduction

What is the common ground for a science of diagrams? It cannot be the prescription of research methods, because our community gains strength through great diversity in methods. A simple definition of which notations qualify as diagrams is also liable to exclude valuable insights, even were it possible to achieve one. Instead we believe that common ground should be established on a taxonomic basis. A wide range of candidate taxonomies have already been described in several different academic fields. In this paper we propose that previous taxonomies should be treated with more detachment than simply selecting the most inclusive or rigorous to be extended as necessary. We propose a set of taxonomic dimensions which can be used as the basis for new taxonomies of diagrams, and can be used to compare and contrast the research interests of different fields contributing to the science of diagrams.

We have used the approach of Organizational Domain Modeling (ODM), a methodology proposed by Simos et. al. (1996). ODM is intended for use in situations where competing interest groups need to share the same information structures. It recognises that no single structure will meet all requirements. Instead ODM identifies commonality and variability between interest groups, and between existing work products that might be reused. In the present study, the interest groups we have considered are the different academic disciplines interested in diagrams. The reusable work products are the various taxonomies that have been proposed in the past. Although derived through a taxonomic process (as implied by the title), the result of this study is not intended to be used as a new "super-taxonomy". We wish to encourage continued diversity in taxonomic analyses of diagrams, and hope to do this by pointing out the range of options that are available. This project is presented as a work in progress; we have made our contextual assumptions as explicit as possible, so that the framework might be expanded in future.

We do not have space here to describe individual taxonomies in any detail, nor to assess their relative advantages. We recommend the original sources listed in the bibliography. Most of the taxonomies have been proposed in a small range of contexts. An example is that of software engineering notations, including both diagrams used for system design (Martin & McClure 1985, Newsham 1997) and visual programming languages (Price, Baecker & Small 1992). The ergonomic implications of these diagrams have been categorised in the Cognitive Dimensions of Notations (Green and Petre 1996). Further examples include the selection of representations for educational contexts (Dale 1969, Goldsmith 1984, Cox and Brna 1995), or in cartography, typography, and graphic design (Bertin 1981, Twyman 1979, Richards 1984, MacDonald-Ross 1977, Garland 1979, van der Waarde 1993, Engelhardt 1998).

The study of aesthetics and representation often generates taxonomic distinctions (Goodman 1968, Ittelson 1996), as do theories of language (Werner & Kaplan 1963). Psychologists investigate the notational factors underlying cognitive performance both to gain insight into performance (Barnard and Marcel 1978, Bennett and Flach 1992, Hardin 1981), but also as a basis for more general theories of cognition (Larkin and Simon 1987, Scaife & Rogers 1996, Zhang 1997). Some recent reviews have attempted to place previous research into diagram use within a framework of these cognitive questions (Blackwell 1997, Tversky 1997).

The Taxonomic Dimensions

The taxonomic dimensions that we propose are presented in table 1. These have been derived from our characterisations of different research interests, which are summarised in Appendix A.

1	The representation (the graphic display)
	1.1	The graphic domain (graphic vocabulary)
	1.2	Graphic structure (visual/spatial relations)
2	The message (the represented information)
	2.1	The information domain (ontological categories)
	2.2	Information structure (relational properties)
3	Relation between representation and message
	3.1	Pictorial correspondence (realistic/abstract)
	3.2	Analogical correspondence (structure mapping)
4	Task and process (interpreting and modifying representations)
	4.1	Information processing (perception and problem solving)
	4.2	Tools (interaction with the representation)
5	Context and convention (cultural and communicative context)
	5.1	Communicative context (roles in discourse)
	5.2	Cultural conventions (society and representation)
6	Mental representation (diagrams in the head)
	6.1	Mental imagery (nature of internal representations)
	6.2	Interpersonal variation (differences between people)

Table 1: The dimensions

Description of the dimensions

The representation - Graphic structure is the most commonly found organising principle in diagram taxonomies, and is central to disciplines such as graphic design. It describes the organisation of the display - distribution of ink and colour. It is usually convenient to separate this description into consideration of individual marks or components ( graphic vocabulary ), and the way those components are related to each other ( graphic organisation ) - even though the definition of a 'component' may vary in different taxonomies.

The message - The information represented by the diagram also has structure. Many taxonomies find it sufficient to describe this structure, the graphical structure, and the type of mapping as a complete description of diagram types. Informational structure is defined in terms of the relationships present in the data (eg. ordinal and relational), although the potential kinds of relationship are often derived from ontological categories (time, space, quantity) that constrain their variation.

Relation between representation and message - As a sign system, the diagram signifies information that is related to its graphic structure. The way in which this is achieved may be described as a mapping process, defining a correspondence between the graphical structure and its interpretation. The correspondence may also require interpretation beyond simple mapping of structure, varying with the extent to which it is pictorial, or the extent to which it involves structural analogy.

Task and process - In a taxonomy that considers how the diagram is used (a science of thinking-with-diagrams rather than simply a science of diagrams), the processes of construction and interpretation must also be considered. Some of these processes are "internal" cognitive processes, while some appear to depend completely on physical devices or tools. In fact, processes of diagram use form a continuum of physical and cognitive operations which is divided only at the peril of the taxonomist. Some taxonomies emphasise particular portions of this continuum (ergonomics, or mental reasoning), but we include them all here.

Context and convention - Diagrams are not self-sufficient. Despite occasional naive claims regarding their inherently intuitive nature, the way that we interpret depictive conventions depends on cultural context as well as the conventions of particular media types. Analysis of a diagram must consider which information is present in the diagram, and which comes from other sources. In any communication, moreover, diagrams are almost always supplemental to other information, and their content must be considered in terms of this discourse context.

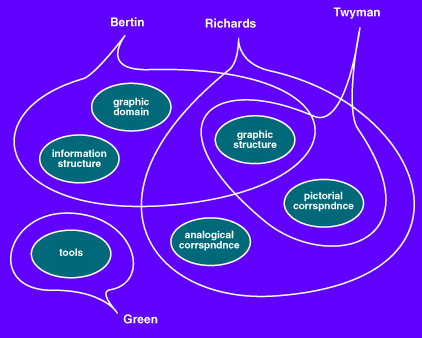
Figure 1: Example of taxonomy overlap

Mental representation - Finally, we have found it necessary to consider mental representation independently from mental process. We do this with some reluctance, but only because so much previous research has emphasised supposedly static properties of mental representations. In this 'purely' mental dimension, we also include those differences between mental representations - between different people, for example - that appear to have some constancy independent of any specific diagram or information context.

Relation to existing taxonomies

The distinctions made in an existing taxonomy may involve several of these taxonomic dimensions. For example, Twyman's (1979) "schema for the study of graphic language" explores "method of configuration" (dimension 1.2) as well as "mode of symbolization" (dimension 2.1). Figure 1 illustrates a few of our taxonomic dimensions, showing how multiple dimensions have been addressed in existing taxonomies.

For each of the existing taxonomies that we have reviewed, table 3 lists the taxonomic dimensions that they consider. This table can be used in two different ways:

1. Existing taxonomies (listed on the left) can be compared with respect to the taxonomic dimensions that they explore.
2. For each taxonomic dimension (listed at the top), those taxonomic systems that have explored this dimension can be found.

There are some apparent clusters of similar taxonomies in this table - these generally represent a specific research tradition, with some taxonomies produced by students of earlier authors for example. There are also some dimensions that tend to be addressed together: 1.2 and 3.1, for example, and 1.2. and 2.1.

	Taxonomic dimensions
Researchers	The representation		The message		Relation/ correspondence		Task and process		Context and convention		Mental represention
Barnard & Marcel					3.1
Bennet & Flach	1.1					3.2	4.1
Bertin	1.1	1.2	2.1
Blackwell											6.1	6.2
Bowman	1.1	1.2
Cox & Brna							4.1
Dale							4.1
Doblin	1.1		2.1		3.1				5.1
Eco						3.2
Engelhardt		1.2
Garland				2.2
Goodman					3.1
Green & Petre								4.2
Hardin		1.2	2.1
Harrison		1.2
Ittelson					3.1
Karsten				2.2
Knowlton		1.2
Larkin & Simon				2.2			4.1
Macdonald-Ross									5.1
Martin & McClure								4.2
Newsham	1.1
Owen		1.2	2.1	2.2		3.2
Rankin		1.2	2.1
Richards		1.2			3.1	3.2
Roth et al.	1.1	1.2	2.1	2.2				4.2
Scaife & Rogers							4.1.					6.2
Tversky			2.1		3.1	3.2				5.2
Twyman		1.2			3.1
van der Waarde		1.2			3.1
Wehrend & Lewis			2.1
Werner & Kaplan						3.2
Wexelblat		1.2	2.1
Zhang							4.1
	The representation		The message		Relation/ correspondence		Task and process		Context and convention		Mental represention

Table 2: Relation to existing taxonomies

Example: The London Underground Diagram

This section provides an illustration of some of the proposed taxonomic dimensions. For each dimension, we mention some specific distinctions that have been (or might be) included in an actual taxonomy, using the London Underground diagram as a familiar example.

Regarding the representation, Bertin's (1967,1977) analysis of the graphic domain would suggest that the Underground diagram uses two implantations: points (the stations) and lines (the connections). These encode information through two of Bertin's graphical variables: shape (types of stations), and color (different lines). Bowman (1968) would identify the same form vocabulary in the Underground diagram as Bertin: point, line, shape, and color . Bertin's analysis of graphic organisation would distinguish three impositions on the plane : diagrams , networks , and topographies . In his framework the Underground diagram would be a hybrid of a network (transcribing relationships among the elements of a single set) and a topography (an ordered network, e.g. a map, copying an arrangement of elements in the physical world). Knowlton (1969) points out three "parts" of a visual representation: the elements (here: the stations), their pattern of arrangement (here: the position on the page), and their order of connection (here: accomplished by the colored lines). Richards (1984) discusses the mode of organization , and points out linking (see the lines) and grouping (see the colors) in the Underground diagram. Wexelblat (1991) distinguishes absolute dimensions (unary properties of objects, can be described based on the examination of each object in isolation) and relative dimensions (properties that can be determined only by examining relationships among the objects). In the Underground diagram, the lines connecting the stations are an example of a relative dimension.

Regarding the message , the Underground diagram is a topological graph, in which the nodes are stations and the arcs are potential routes of travel between stations. The ontological status of the message might be regarded as consisting solely of this topological information, or it might represent a sequence of actions required to reach a particular destination, or a geographical map. The pictorial correspondence in the relation between representation and message is classified by Twyman (1979) as using a schematic mode of symbolization. Richards describes the mode of depiction of the Underground diagram as non-figurative . The analogical correspondence, according to Knowlton, would be a logical picture (elements are arbitrarily portrayed, while pattern and/or order of connection are isomorphic with the state of affairs represented), as opposed to a realistic picture (iconic elements), or an analogical picture (indirect reference through analogical/metaphorical relations). Richards classifies the mode of correspondence of the Underground diagram as semi-literal . Eco (1985) points out that the Underground diagram is at once iconic (in its use of space to stand for space) and symbolic (in its use of straight unidimensional lines to stand for the fragmented route of the tracks).

There has been less empirical investigation of the Underground diagram, but the taxonomic dimensions suggest several areas of investigation that might have been carried out. The perceptual attributes of the diagram, including line weights, colour discrimination, font legibility and so on are essential to its usability. We can conjecture about interaction with the representation on the basis that maps in the underground are worn out in a patch near the current station. Users presumably put their finger on that patch, then trace a route to where they want to go. The finger is an interaction tool that is an essential component of the notational system. The Underground diagram also has a complex cultural and communicative context . When the diagram is printed on a T-shirt, what is its diagrammatic function? This iconic use of the diagram represents a special cultural convention: the Underground diagram can also be used as a substrate for other messages. For example, shops in London often use a customised version of the diagram in their advertisements, to highlight their location. The Underground diagram has also affected mental representations : according to Garland, it has changed people's mental map of distances across London. No doubt the many versions also accommodate interpersonal variation - versions for use by the visually impaired, for example.

Some of the taxonomies that we have reviewed do not easily accommodate the Underground diagram. Rankin's (1990) taxonomy of graph types focuses "only on those graphic forms which utilize a co-ordinate space. That is, the dimensions of the picture are explicitly stated and numerically scaled." The Underground diagram falls outside the scope of his taxonomy. Lohse et al. (1994) propose a classification of visual representations based on how their experimental subjects rated and sorted a set of sixty examples of visual representations. However, the Underground diagram does not seem to fit into their classification system: strictly speaking, it is neither a map ("Maps are symbolic representations of physical geography. Maps depict geographic locations ..."), nor a structure diagram ("The spatial data expresses the true coordinate dimensions of the object."), nor a network chart ("The planar coordinate system of network charts is generally void of meaning", "network charts present nonspatial information ..."). If the Underground diagram had been included in their experimental data set, the results may have given an interesting insight into its cultural implications.

Discussion

Several other researchers have proposed classifications of existing diagram taxonomies. A common distinction (Rankin 1990, Lohse et al. 1994) is between functional taxonomies and structural taxonomies. Functional taxonomies involve our taxonomic dimensions of task and process, and our dimensions of context and convention. Structural taxonomies involve our taxonomic dimensions of graphic structure and information structure. However, several of the taxonomic dimensions discussed in this paper fall outside the functional/structural distinction: mode of signification, information domain, and mental representation. Furthermore, since some taxonomic systems (e.g. Bennet & Flach, Doblin) involve both functional and structural dimensions, they also do not fit into the functional/structural dichotomy.

Goldsmith's (1984) work is similar to ours in the sense that she is also trying to create a high-level reference frame for positioning and discussing existing research on visual representation. Her work is quite different to ours in the sense that the existing research that she is looking at is not about diagrammatic representations and their use, but about depictive illustration, including issues of object identification and perception of pictorial depth. Her taxonomic dimensions are geared towards those issues. In addition, the existing research work that she is studying and structuring is not taxonomic in nature, as in our case, but empirical.

Lohse et. al. (1994) have also produced a widely cited taxonomy of visual representations. This taxonomy is not based on an academic review, however, but on similarity assessments made by experimental subjects for a sample of typical visual representations. This is a valuable exercise, but it is not a substitute for principled analysis. If anything, the whole project falls within our dimension 5.2. - it was a study of public attitudes toward representations rather than their intrinsic characteristics.

In our survey, it is clear that the majority of the previously proposed taxonomies in diagram research fall into the first few of our taxonomic dimensions. These dimensions concern formalisable structure, and the attributes of diagrams that are most apparent by inspection. The first three dimensions also fit most easily within the framework of semiotics, although that does include the pragmatic contexts in dimensions 5.1 and 5.2. Our characterisation of outstanding research issues, however, is generally grouped toward the later dimensions. These dimensions concern questions of performance, interpretation and cognition.

The reasons why taxonomies have tended to ignore these later issues is also clear - they are less easily formalised. We must ask ourselves, though, whether this neglect is either desirable or necessary. As Ittelson points out, diagrams have no meaning without an interpreter and a communicative intent. There are many academic disciplines which quite reasonably give separate consideration to those questions more amenable to formal analysis. Contextual issues require different research methods, even different academic disciplines.

An interdisciplinary science of thinking with diagrams, such as the one proposed by this workshop, cannot afford to concentrate only on formal analyses without context. We hope that the taxonomic framework we have proposed here will be developed further, and that it will provide some guidance to those areas in which previous taxonomies have been weakest and those in which future research will be most valuable.

Appendix A: Characterisation of research interests

This appendix summarises the research interests and objectives of the different academic fields that we identified as the basis for our taxonomy. Our knowledge of some of these fields is not as intimate as we would like, and we have almost certainly distorted their positions according to our own biases. This is the principle reason why we wish to consider this as a work in progress, and look forward to feedback in the course of the workshop.

Applied psychology. How do different diagram types and diagram features affect human problem solving? It is clear that a wide range of cognitive tasks are involved in constructing and interpreting diagrams, but we are not necessarily able to enumerate them or characterise them. If we could do so, we would be able to propose ways to make the use of diagrams faster, more accurate or easier to learn. These applied objectives have further scientific implications, however. Investigating the use of diagrams can teach us about the nature of cognition; this is central to the traditional concerns of cognitive psychology with perception, memory and problem solving.

Cognitive science is already focused on definite descriptions of diagrammatic reasoning tasks. As with all cognitive science, the use of computer models allows researchers to propose and investigate systematic (and potentially formalisable) models of reasoning. A primary focus of research into reasoning with diagrammatic representations is to investigate how these models can accommodate analog representations rather than symbolic logic. Cognitive scientists carry out formal analyses of these different types of representations, but are also concerned with the nature of "internal representations" in human reasoning - the long standing debate over mental imagery, for example, is regularly informed by research into diagrams. A further product of cognitive science research is that of artificial intelligence - what can we discover about computational questions or engineering solutions by building computer systems that use analogue representations?

Linguistics. How can the syntax, semantics, and pragmatics of diagrams be analysed? Modernist structural analysis has given us all a passing familiarity with Saussure's trichotomy; this was evident from the similarities between the taxonomies that we compared. Computational linguistics, however, is concerned with properties of diagrams that enable research analogous to the research on verbal language. How can we formulate grammars that will allow automatic parsing and generation of diagrams? How can we write and test those grammars, or use them to analyse the structure of discourse? Situational semantics considers communication in a context that includes artefacts such as diagrams, and allows statements to be made about the informational status of the whole situation. How can we apply theories of conversational implicature to diagrams? What does the viewer expect a diagram to mean, and how can the producer exploit that expectation?

Visual programming. Diagrams have held promise as a means of programming computers for many years. The objective is egalitarian - will diagrams make programming accessible to more people? This may be social - encouraging communication between programmers and their managers; educational - providing notations usable by children; or democratising - making programming accessible to novices rather than experts. How can these be achieved? Early work was unreasonably optimistic about the value of diagrams, and much research is now focused on using Green's cognitive dimensions of notations to assess suitability for different tasks. Educational use of visual programming implies that skills learned from diagrams can be transferred to other notations - is this true? We need to understand what the user is learning - is it a virtual machine, mathematical properties of an algorithm, or just execution statistics? Finally, the traditional concerns of computer science intersect with these properties of diagrams. How can they be parsed and executed efficiently, and will they "scale up" to large and complex problems?

Data visualisation. Most diagrams are created by a person with a communicative intent and an understanding of the expected reader. How can data be characterised and design rules formalised in order to automate the creation of visual representations? This might involve choosing an appropriate interpretation of higher-dimensional data in two or three dimensions - if three, how can we deal with the occlusion problem on a visual display screen? How can such a system choose to allocate dimensions to isomorphic representation of physical spaces rather than symbolic information? What is the space of possible visual interactions between the user and the machine? Will we facilitate deeper understanding by making diagrams interactive or immersive? In all of these considerations, we need to know how the choice of an appropriate visualisation depends on the user's information seeking goals.

Graphic design. The task of a graphic designer is to accept a given set of information, and prepare a way of communicating that information effectively. In order to do this, they must have access to some set of possible design solutions. How can this set be systematised? What is the visual vocabulary available to the designer? These are the topics of research in graphic design. The visual vocabulary must be extended by a 'space' of possible spatial organisation (set-up, lay-out) for a given design problem. Graphic design also takes place within a social context: how does the genre (instructions, signage, newspaper graphics, textbook illustration, forms, etc.) affect design decisions beyond the simple limitations of media type and the trivialities of graphical fashion?

Education. Which types of diagrams are appropriate for what teaching goals? The field of education considers two separate questions: firstly, the need to educate children to be graphically "literate". What are the requirements of graphical literacy, how can it be assessed, and at what age should it be taught? Does it belong within a specific subject (e.g. mathematics), or should it span the curriculum? The second objective in education research is to understand how use of diagrams can facilitate education in all subjects. When and how and to what extent should we use diagrams in a textbook or a classroom presentation? Are they likely to enliven dull material, or will students ignore them as overly technical? If concepts are learned diagrammatically, can this inhibit the development of abstract concepts?

History and philosophy of science. Scientific discovery has often been associated with novel uses of representations. Some of these involve representations that are now widespread, such as algebra or Cartesian coordinates, while others were completely personal (Einstein's thought-experiments, or Kekule's insight into the structure of the benzene ring). Are representations essential to science? Classicists such as Reviel Netz are doing "cognitive history" by investigating the diagrams on which past discoveries have been founded. The narratives of creative discovery from scientists bear great resemblance to architectural theories of creative sketching. Is such creativity restricted to intellectual giants, or can ordinary people exploit these diagrammatic strategies in the course of problem-solving?

Architecture. Architects spend much of their time working with visual representations. Some of these are described by the architects themselves as diagrams, although their most common representation is the sketch. The uses of sketches are closely related to the uses of diagrams, however. How can a broader definition of diagram types support architectural problem solving? Are there some representations which constrain the possible design solutions? This is an issue of major concern whenever architects use computer aided design tools. Alternatively, what sort of diagrams facilitate the creativity that architects experience when sketching? Research into architectural sketching provides a radically different perspective on the cognitive function of diagrams, although one that has been also discovered in studies of software engineers.

Decision support. Although we are aware that researchers in decision support are interested in many of the issues raised here, neither of us feel sufficiently qualified to make any statements about their research objectives. We have therefore noted the existence this topic, but will consider it no further here. We look forward to meeting some decision support researchers at the conference in order to learn more!

Appendix B: Coverage of the domain

How well do our taxonomic dimensions accommodate the research interests and taxonomies from which they are derived? This paper is too brief to allow a full discussion of the taxonomies, or of specific research interests (which are briefly reviewed in Appendix A). We simply summarise the progress we have made in table 3. This lists some of the terminology defined in existing taxonomies, in order to illustrate how they fit within our dimensions, and we contrast these with the research interests described in Appendix A. Note that, although we refer to individual dimensions in each taxonomy, these are often combined into a matrix or some other multi-dimensional scheme by the original authors.

Dimension	Existing taxonomies	Research interests
1. The representation
1.1. The graphic domain (graphic vocabulary)
	Bennet & Flach, "visual features" Bertin, "implantations: point, line, area" Bertin, "visual variables: position, size, color, ..." Bowman, "form vocabulary: point, line, shape, color, ..." Doblin, "verbal, numerical, visual" Newsham, "visual vocabulary" Roth & Mattis, "graphemes: mark, line, bar, text,..." Roth & Mattis, "grapheme properties: color, size, ..."	available visual vocabulary
1.2. Graphic structure (visual/spatial relations)
	Bertin, "impositions on the plane: diagram, network, map" Bowman, "spatial grammar: superimposition, chiaroscuro..." Engelhardt, "generative spatial grammar: axis, links, ..." Hardin, "linearity, order, continuities, geometry" Harrison, "levels of structure: "pict, picteme, ..." Knowlton, "elements, their arrangement, their connection" Owen, "sequential, presentational" Rankin, "dimensions: number of, linear, circular, ..." Richards, "organisation: grouping, linking, variation" Roth & Mattis, "layout: chart, table, map, network, ..." Twyman, "configuration: from pure linear to nonlinear" van der Waarde, "relations between graphic components" Wexelblat, "absolute dimensions, relative dimensions"	space of possible spatial organisation (setup, layout) diagram grammars scalability
2. The message
2.1. The information domain (ontological categories)
	Garland, "action, force, process, proposition, ..." Karsten, "space, idea, time, composites, change, ..." Larkin & Simon, "spatial, artificial" Owen, "space, time, domain" Roth & Mattis, "time, space, temperature, mass, ..."	are representations essential to science
2.2 Information structure (relational properties)
	Bertin, "selective, ordered, quantitative, ..." Doblin, "nominal, noumenal, phenomenal" Hardin, "explicitness, structure, complexity" Owen, "discrete, order, continuous" Rankin, "number of variables, function, ..." Roth & Mattis, "nominal, ordinal, quantitative, ..." Tversky, "nominal, ordinal, interval, ratio" Wehrend & Lewis, "identification,categorization, ranking, ..." Wexelblat,"linear, ray, quantum, nominal, ordinal, ..."	representational constraints on design computer systems with analog repns
3. Relation between representation and message
3.1. Pictorial correspondence (realistic/abstract)
	Barnard & Marcel, "abstract depictive" Goodman, "characters: distinct analog" Ittelson, "designs, writings, diagrams, depictions" Owen, "symbolic, analogic, iconic" Richards, "depiction: from figurative to non–figurative" Tversky, "metonymy, synecdoche" Twyman, "symbolization: verbal/numer., pictorial, schematic" van der Waarde "verbal, pictorial, schematic, composite"	difference between sentential/analogue
3.2. Analogical correspondence (structure mapping)
	Bennet & Flach, "mapping: categorical, elemental, hierarch." Richards, "correspondence: from literal to non–literal" Tversky, "metaphor, cognitive correspondence" Werner & Kaplan, "symbols derived from their affective qualities"	analogies to verbal language
4. Task and process (interpreting and modifying representations)
4.1. Information processing (perception and problem solving)
	Bennet & Flach, "cues, memory, system control" Cox & Brna, "cognitive and semantic properties" Dale (educational context) Larkin & Simon, "search, inference, perception" Scaife & Rogers, "offloading, re-representation, constraining" Zhang, "lookahead, knowledge, perceptual bias"	representational constraints on design learning abstract concepts cognitive tasks in construction and interpretation nature of perception and problem solving choosing a visualisation for information goals understanding virtual machines making diagrams faster/more accurate/easier to learn
4.2. Tools (interaction with the representation)
	Chuah & Roth, "semantics of visualization interactions" Green, "cognitive dimensions" Martin & McClure, "desirable properties of notations"	tradeoffs and design maneouvers space of possible visual interactions occlusion problem in 3D graphics
5. Context and convention (cultural and communicative context)
5.1. Communicative context (roles in discourse)
	Doblin, "information, persuasion, stimulation" Macdonald-Ross,"iconic, data display, explanatory, operational"	when to illustrate a textbook diagrams with verbal presentations structure of discourse
5.2. Cultural conventions (society and representation)
	Tversky, "cultural neutrality Scaife & Rogers, "convention, canonical forms" (but better to have anthropological categories)	what constitutes graphical "literacy"? diagrams in a social context genre and design decisions applying conversational implicature
6. Mental representation (diagrams in the head)
6.1. Mental imagery (nature of internal representations)
	Blackwell, "categorical, coordinate" Blackwell, "verbal, visual"	research into nature of memory nature and status of internal representations how do diagrams facilitate creativity? transfer of strategic knowledge between representations
6.2. Interpersonal variation (differences between people)
	Blackwell, cognitive style "verbaliser-visualiser" Blackwell, handedness / hemispheric specialisation Blackwell, gender differences Scaife & Rogers, "practice, familiarity"	making diagrams suitable for novices or children what age to teach diagram use is problem-solving like scientific discovery

Table 3: Coverage of the domain

Acknowledgements

We would like to thank Peter van Emde Boas, Ingrid von Engelhardt, Theo Janssen, Karel van der Waarde, and Alan Swanson for their helpful comments on an earlier draft of this paper.

Alan Blackwell's research is funded by a collaborative studentship from the Medical Research Council and Hitachi Europe Ltd. He is grateful to the Advanced Software Centre of Hitachi Europe for their support.

Yuri Engelhardt's research is funded by the Dutch National Institute of Public Health and the Environment.

References

Bennett, K.B. & Flach, J.M. (1992). Graphical displays: Implications for divided attention, focused attention and problem solving. Human Factors, 34(5), pp. 513-533.

Bertin, J. (1967). Semiologie graphique: les diagrammes, les rseaux, les cartes. Mouton and Gauthiers-Villars, The Hague, Paris.

Bertin, J. (1981). La graphique et le traitement graphique de l'information. Flammarion, Paris.

Blackwell, A.F. (1997). Diagrams about thinking about thinking about diagrams. In M. Anderson (Ed.), Reasoning with Diagrammatic Representations II: Papers from the AAAI 1997 Fall Symposium. Technical Report FS-97-02. AAAI Press, Menlo Park (CA), pp. 77-84.

Bowman, W.J. (1968). Graphic Communication. New York: John Wiley.

Chuah, M.C., and Roth, S.F. (1996). On the Semantics of Interactive Visualizations, Proceedings of Information Visualization, IEEE, San Francisco, October 1996, pp. 29-36.

Cox, R. & Brna, P. (1995). Supporting the use of external representations in problem solving: the need for flexible learning environments . Journal of Artificial Intelligence in Education, 6(2), pp. 239-302.

Doblin, J. (1980). A structure for nontextual communications. In P.A. Kolers, M.E. Wrolstad & H. Bouma (Eds), Processing of Visible Language 2. New York: Plenum Press. pp. 89-111.

Eco, U. (1985). Producing signs. In: M. Blonsky (ed.), On Signs. Baltimore: John Hopkins University Press, pp. 176-183.

Engelhardt, Y. (1998). Meaningful space: How graphics use space to convey information. Proceedings Vision Plus 4, School of Design, Carnegie Mellon University, Pittsburgh, pp. 108-126.

Garland, K. (1979). Some general characteristics present in diagrams denoting activity, event and relationship. Information Design Journal , 1(1), pp. 15-22.

Goldsmith, E. (1984). Research into illustration: An approach and a review. Cambridge: Cambridge University Press.

Green T.R.G. & Petre M. (1996). Usability analysis of visual programming environments: a "cognitive dimensions" approach. Journal of Visual Languages and Computing, 7, pp. 131-174.

Hardin, P. (1981). Representational characteristics in diagrams of statements of relationships. Unpublished PhD thesis, University of Iowa, UM 812 8401.

Harrison, R.P. (1964). Pictic analysis: Toward a vocabulary and syntax for the pictorial code; with research on facial expression. Unpublished PhD thesis, Michigan State University.

Karsten, K.G. (1923). Charts and graphs. New York: Prentice-Hall.

Knowlton, J.Q. (1966). On the definition of "picture". AV Communication Review, 14, pp. 157-183.

Larkin, J.H. & Simon, H.A. (1987). Why a diagram is (sometimes) worth ten thousand words. Cognitive Science, 11, pp. 65-99.

Lohse, G.L., K. Biolisi, N. Walker, H.H. Rueter (1994). A classification of visual representations. Communications of the ACM, 37(12), pp. 36-49.

Macdonald-Ross, M. (1977). Graphics in texts. In: Shulman, L.S. (ed), Review of research in education, Vol. 5, Itasca, Ill.: Peacock.

Martin, J. & McClure, C. (1985). Diagramming techniques for analysts and programmers. Englewood Cliffs, NJ: Prentice-Hall.

Newsham, R. (1995). Symbolic representation in object-oriented methodologies: Modeling the essence of the computer system. Unpublished Master's thesis, Department of Computer Science, Nottingham Trent University.

Owen, C.L. (1986). Technology, literacy, and graphic systems. In: Wrolstad, M.E. and Fisher, D.F., Towards a new understanding of Literacy. Proceedings of the third conference on Processing of visual language, held May 31 through June 3, 1982, at Airlie House, Airlie, Viginia.

Price, B.A., Baecker, R.M. & Small, I.S. (1993). A principled taxonomy of software visualization. Journal of Visual Languages and Computing, 4(3), pp. 211-266.

Rankin, R. (1990). A taxonomy of graph types. Information DesignJournal, 6(2), pp. 147-159.

Richards, C.J. (1984). Diagrammatics. Ph.D. thesis, Royal College of Art, London.

Roth, S.F., M.C. Chuah, S. Kerpedjiev, J.A. Kolojejchick, and P. Lucas (1997). Towards an information visualization workspace: Combining multiple means of expression. Human-Computer Interaction, 12(1&2), pp. 131-185.

Roth, S.F. & Mattis, J. (1990). Data Characterization for Intelligent Graphics Presentation, Proceedings of the Conference on Human Factors in Computing Systems (SIGCHI '90), Seattle, WA, April 1990, pp. 193-200.

Scaife, M. & Rogers, Y. (1996). External cognition: how do graphical representations work? International Journal of Human Computer Studies, 45, pp. 185-214.

Simos, M., Creps, R., Klingler, C., Levine, L. & Allemang. D. (1996). Organization Domain Modeling (ODM) Guidebook, Version 2.0. STARS Technical Report STARS-VC-A025/001/00, Lockheed Martin Tactical Defense Systems, Manassas VA, June 1996.

Tversky, B. (1997). Cognitive principles of graphic displays. In M. Anderson (Ed.), Reasoning with Diagrammatic Representations II: Papers from the AAAI 1997 Fall Symposium. Technical Report FS-97-02. AAAI Press, Menlo Park (CA), pp. 116-124.

Twyman, M. (1979). A schema for the study of graphic language. In: P.A. Kolers, M.E. Wrolstad, H. Bouma (Eds.), Processing of visible language. Vol. 1. New York: Plenum Press, pp. 117-150.

van der Waarde, K. (1993). An investigation into the suitability of the graphic presentation of patient package inserts. Unpublished PhD thesis, Department of Typography and Graphic Communication, University of Reading, UK.

Wexelblat, A. (1991). Giving meaning to place: semantic spaces. In: M. Benedikt (Ed.), Cyberspace: first steps. MIT Press, pp. 255-271.

Wehrend, R. and Lewis, C., A problem-oriented classification of visualization techniques. In: Proceedings of the first IEEE Conference on Visualization: Visualization 90, pp. 139-143. IEEE, Los Alamitos, CA, October 1990.

Zhang, J. (1997). The nature of external representations in problem solving. Cognitive Science, 21(2), pp. 179-217

Click to return to Alan Blackwell's home page.