Originally published March 1989
Knowledge-Based Systems, 2(1), 37-45.
Apologia for Web readers(1996): I no longer agree with everything I wrote eight years ago. This paper seems rather dated to me now, and I certainly hope that my prose style has improved! Nevertheless, there are some ideas here that are peripherally relevant to my current interest in spatial representations, and that are of interest to other people working on related topics. The journal in which this paper appeared is very hard to obtain, so I make the text available here in the same form as it originally appeared.
A qualitative representation for shape and space in two dimensions, and methods for carrying out simple spatial reasoning tasks using this representation are described. The representation provides facilities that enable qualitative physics systems to use qualitative methods not only at the process level, but also at the constraint and motion analysis level. It also provides qualitative methods that could be applied to conventional spatial reasoning applications, such as high level robot programming.
Keywords: qualitative physics, spatial reasoning, robot programming
New approaches to automated spatial reasoning are largely driven by the problems of robotics. Although today's robots developed out of the field of Artificial Intelligence (AI), they are ironically most limited by their reasoning abilities. Robots are physically versatile, to an extent that makes them at least comparable to humans, and they can theoretically be reconfigured for a wide range of tasks. In practice, reconfiguration is expensive, because the motion of the robot must be reprogrammed in detail for each new task[1]. If robots were more adept at spatial reasoning, the range of robot applications could expand dramatically as a result of reductions in these programming expenses.
Many researchers have addressed the problems of robot reasoning, especially over the last 15 years. As with most AI applications, much of the work has involved designing appropriate representations for the knowledge that robots work with. The project described in this paper takes a new approach to knowledge representation in the robot domain by investigating spatial reasoning using a purely qualitative representation.
Analysis of physical problems using qualitative reasoning techniques has already been addressed by the field of qualitative physics. This field has to date concentrated on qualitative analysis of process, rather than qualitative analysis of shape or space. A representation for qualitative spatial reasoning can therefore extend current techniques in qualitative physics, as well as providing a new technique for robot reasoning.
The tasks which have been performed using the qualitative reasoning techniques developed in the current project are only a small subset of general problems in robotics or in qualitative physics. They are, however, genuinely useful tasks. A system which can reason about interaction of objects sliding past each other, and can solve simple cases of the "piano mover's problem" - a simple path planning exercise - in two dimensions is described below.
The development and properties of the qualitative representation used to solve these problems is also discussed below. This is preceded by discussions of reasoning and representation techniques used in a number of spatial reasoning systems, and in qualitative reasoning systems. Finally, the possible contribution of qualitative spatial reasoning, both to the field of robotics and to qualitative physics research, is evaluated.
The two fields which include most research in spatial reasoning are those of robotics and machine vision. These two are often closely related, since robots rely on sensory data that may be provided by a vision system, and a long term goal of vision research is to guide autonomous robots. This section gives a brief survey of the types of reasoning and representation techniques used in these fields.
A considerable research effort has been devoted to each of these levels of abstraction in robot systems, and several projects have investigated organization models for integrated systems stretching across all these levels. The levels at which qualitative reasoning techniques might be appropriate are the latter three, because they deal with the type of problems which humans solve qualitatively - problems of motion and control, although we perform them unconsciously, require many numeric calculations when performed by a robot.
The majority of today's commercial robots are programmed at the robot-level. The only spatial representation necessary to support this type of programming is a stored description of joint angles, workspace coordinates, forces to apply, etc. These components are often combined in a trajectory which describes a sequence of positions, motions or forces in multiple dimensions. This representation is very limited in supporting reasoning, since the workspace is only partially implicit in a trajectory (e.g. in the way that the shape of the car is implicit in the path of a spray painting robot).
Many early (1970s) robot reasoning projects used space filling spatial representations. In these systems an area of space (either the workspace or just the visual field) is partitioned into small parts, each of which is classified as either occupied or unoccupied. An object in a scene is represented simply as a collection of occupied regions. In many early vision-guided systems, the space partitions corresponded to pixels in a visual image[7], thereby ensuring great simplicity in the construction of the representation from sensory data.
Space filling representations suffer from the same efficiency problems as bitmapped graphics, although like bitmaps they can be made more memory efficient by quadtree methods[8], and more accurate by fitting partition edges to object edges[9]. They do have an advantage in that empty space is explicitly represented (this is useful for path planning), but they do not perform well where objects are not aligned with the division of space. They are also difficult to use where complex scenes are involved, because it is not easy to distinguish where multiple objects are joined, or overlap.
The drawback of space filling techniques is that the boundaries of objects are not explicitly described, while all interaction with objects does take place on the boundary. Practical robot systems have often included the design of boundary descriptions that are customized for particular types of object - fancy chocolates in one case[10], or sheep in another[11]. A more general technique for basing object descriptions on the object boundary is the smoothed local symmetry method[12], which partitions an object into components identified from discontinuities and other shape cues in the boundary.
Developments in robot programming require the use of a representation that is convenient for humans to work with, as well as convenient for robot reasoning. Task level and goal level robot programming has often made use of Constructive Solid Geometry (CSG) techniques for describing objects that the robot will be working with, as in the AUTOPASS[13] and RAPT[6] projects. Such representations can be very complex when compared to the level at which the robot operates, and must be translated from the level at which the programmer works to the level at which the robot acts. This translation can be a complex geometric exercise.
Some of the more common approaches to spatial representation for robot reasoning have been described, but this is by no means exhaustive. Many projects have included spatial representations, although most of these could be broadly classified as based on either space filling, boundary description, component structure or solid modelling.
There are many types of computer system which must represent spatial information, but do not need to carry out any reasoning with it. Computer Aided Design (CAD) and computer graphics have both resulted in new spatial representations. Techniques from these fields have been borrowed from time to time for use in robot reasoning systems. Solid modelling techniques such as wireframe description, boundary representation and constructive solid geometry have all been used for reasoning systems as well as for CAD, and CSG in particular has been applied to robotics.
There exist a variety of solid modelling and shape description techniques which have not yet been exploited for use in spatial reasoning, but there are still many candidates, especially where the representation of natural objects is involved, since robot systems presently deal almost exclusively with man-made objects, and use representations that are most suitable for that purpose.
There have been two main streams of research in qualitative reasoning methods for computers, each with a different overall emphasis. One builds on the work of de Kleer[14], and is referred to as qualitative physics, and the other, naive physics, stems from initial proposal by Hayes[15].
Although the goals and methods of these two streams are different, they have influenced each other to a high degree, and literature in each stream regularly cites work from the other. The question of spatial reasoning is relevant to both, so each is briefly described here.
The first system described in qualitative physics literature was de Kleer's NEWTON program, which solved Newtonian physics problems. When given a description of a block on a roller coaster, it could predict the motion and final state of the block from qualitative information about the roller coaster: whether given parts of it sloped up or down, or were level.
De Kleer and others extended qualitative analysis techniques to the domains of electronic circuits, hydraulic circuits, and electro-mechanical circuits. In each domain, the qualitative descriptions typically reduce quantity measurement to three qualitative values: positive, zero or negative. Some quite complex dynamic systems can be analysed by including positive, zero or negative first and second derivatives. In all these systems, the emphasis is on reasoning about the behaviour of a system from its structure.
Forbus is another major researcher in qualitative physics who has been involved in a wide range of projects. These include a system which predicts the motion of a bouncing ball in a two dimensional world, and qualitative process theory, a method for analysing dynamic processes in qualitative terms.
A considerable body of research has grown from initial projects by de Kleer, Forbus and others. A representative collection of this research, edited by Bobrow, was published in 1984[16].
The original definition of naive physics was stated by Hayes in the Naive Physics Manifesto[15]. The manifesto describes the overall goal of naive physics as the development of a large-scale formalism of common sense knowledge about the world. This concern with real-world knowledge explicitly rejects the tendency in AI to test new reasoning methods in 'toy-world' situations, where the removal of rich real-world data can completely alter the nature of a reasoning problem.
The Naive Physics Manifesto proposed that a large body of formal knowledge about the everyday world should be compiled before any attempt was made to build programs that operate on that knowledge. Qualitative physics research, although it often cites Hayes, has so far concentrated on the development of qualitative reasoning programs, rather than on real world knowledge, and this is a major divergence in methods between the two fields.
With regard to spatial reasoning, Hayes notes in the manifesto that much naive information about the world involves spatial data, and that spatial information should therefore be a priority of the naive physics programme.
The types of problem addressed by qualitative physics systems have included explanatory tasks (such as finding system function from structure), predictive tasks (such as predicting where a bouncing ball will travel to) and diagnostic tasks (especially in malfunctioning circuits).
Qualitative reasoning methods can also be applied to planning and design problems, although this is not often done, perhaps because these tasks are less constrained.
A feature of many qualitative physics problems is a device and conduit description of the analysed system's structure. A circuit-like system, whether electrical, electronic or hydraulic, can be described in terms of a number of devices, each with one or more ports. The characteristics of the device define known relationships between quantities (such as voltage or flow) at its ports. The ports are connected by conduits, which guarantee equal values for the quantities at each end of the conduit. The behaviour of the system can then be analysed as a function of the device characteristics, the conduit topology, and an initial state or disturbance.
There are two central techniques which distinguish the qualitative physics approach to problem solving: these are the quantity space, and envisionment. The quantity space replaces numeric measurements with a range of qualitative values. The three-valued space {[-] [0] [+]} is the most primitive quantity space, but a quantity space might be divided by 'distinguished points' other than zero; e.g. in a problem involving the heating of water the temperature quantity space might have a distinguished point at each of 0° C and 100° C, and three other qualitative values separated by those points.
Envisionment is a method for analysing the behaviour of a system from its structure. In a system of devices and conduits, the qualitative state of the system can be described in terms of one or more quantity space values at each port of every device in the system. Envisionment predicts how this system state will change when the system is perturbed. A complete envisionment would include a series of states resulting from an initial state, and would constitute a description of the behaviour of the system from which its function might be deduced.
Much qualitative physics research has avoided the issues of spatial reasoning by using the device and conduit abstraction. This abstraction allows the spatial description of a system to be replaced by a purely topological description. It can only be applied to a limited range of physical situations, however, and this has resulted in a limited number of domains for qualitative physics research. There are a few projects that have specifically addressed spatial reasoning questions, most notably in two domains - the bouncing ball world and the mechanism world.
The bouncing ball world described by Forbus[19] is a two dimensional domain, in which a point mass is free to move anywhere between a number of bounding surfaces. The free space between these surfaces is divided into a number of regions by extending dividing lines vertically and horizontally from discontinuities in the surfaces. Forbus calls this division of free space a place vocabulary, and it provides a qualitative basis for describing the position of the ball.
From any one region ('place') the ball can move into a finite number of other regions (at most eight, including diagonals, if there are no neighbouring boundaries). The qualitative state of the bouncing ball is actually a combination of its current position, together with direction of motion, and stored energy. The place vocabulary effectively converts a continuous model of free space into a discrete model, with motion represented only in terms of transitions between nodes in the network of places.
The machine world is a domain in which the qualitative reasoning system analyzes the motion of systems of rigid mechanical components. The interaction between the components includes relative motion, mutual constraint and transmission of kinetic energy.
Machines can be regarded for some purposes as being systems of devices connected by conduits, where the conduits transfer kinetic energy. The devices in this case are kinematic pairs (such as two gears, or a pivot). Joskowicz[17] describes a system which performs analysis of kinematic chains in these terms. This system first analyzes the geometry of the components using numeric methods, in order to identify them as particular kinematic pairs. It then employs techniques like those used for qualitative circuit analysis on the resulting device and conduit description.
Stanfill's MACK system[18] operated in a similar manner, working from a geometric description of mechanical devices. It was not restricted to kinematic pairs, but included process descriptions such as expansion of gases in cylinders. It carried out an initial geometric analysis, and then employed a version of qualitative process theory on the qualitative description derived from geometry.
Forbus, Nielson and Faltings[19] describe the application of the place vocabulary to mechanisms such as a ratchet or a clock escapement. The state of the system is described in terms of contact between the parts, e.g. a change of state might involve the pawl of a ratchet falling between teeth on a gear. The place vocabulary is constructed using a numerical geometry technique originally developed for robot path planning.
The above systems all describe physical situations by performing an initial geometric analysis of possible object interaction, so that the qualitative reasoning component can operate with a topological description of mechanical influences or possible state transitions. The initial preprocessing stage is not a qualitative method, and it can remove the need for the qualitative reasoning component to make any use of spatial information by reducing spatial relationships to logical ones.
The qualitative spatial reasoning system described in the remainder of this paper does qualitative reasoning at a much lower level; the geometric relationships between shapes can be analyzed qualitatively, and space is represented in a continuous manner, rather than being divided into places.
The development of a qualitative representation for shape and space which can be used for qualitative spatial reasoning is described here. There are a number of facilities which are not provided by spatial representations for use by robots, or by qualitative representations, but which are important components in many spatial reasoning tasks encountered by humans. This representation attempts to provide these features, including facilities such as description of shape at multiple levels of detail, independent description of shape in local contexts, and relative size comparisons. At the same time, it attempts to retain the capabilities of current representations for qualitative physics and high level robot reasoning.
Two qualitative representations were developed in the course of this project, and both are described here. (This is both for purposes of comparison, and to demonstrate how the preferred representation was developed.)
Advanced robot programming systems such as AUTOPASS, RAPT or LAMA, have generally used CSG-like solid modelling schemes as the basis for representing shapes of workpieces, tools, and the robot itself. CSG representations seem to be intuitively easy for people to operate with, and are therefore appropriate for use where the descriptions must be created by a programmer.
A number of properties of CSG techniques seem to be useful for qualitative shape representation, and the first representation developed in this qualitative spatial reasoning project was a two dimensional version of CSG with the following features: overall shape can be described as a combination of less complex shapes; the relationships of shapes and subshapes are described by relative orientation of shape axes; and shapes can eventually be decomposed to the level of primitive shape elements.
Overall, shape in this representation was decomposed firstly to subparts, which were convex portions of the overall shape, and then to individual shape features such as vertices, edges and curves. Objects, subparts and features were all specified in terms of unique axes. The relative size of subparts and features was described with respect to the length of axes in the parent shape, and position and orientation was also described relative to those axes.
The relative sizes and positions of complete objects could also be described in terms of their axes. All of these descriptions were made in qualitative terms: size was specified in a local quantity space defined by the axes of the parent shape, and position was stated in terms of half spaces divided by local axes.
This combination of axially specified subparts and features appeared to be similar to the way that human mentally decompose a complex object into simpler parts. An English version of a scene representation could be easily recognized as the type of description that a person would construct naturally.
Although it seemed intuitively to be a reasonable method of describing shape, the complexity of nested subparts and locally axis-relative size and position description made it difficult to use this representation for reasoning about motion and interaction of objects. This was partly because the nested local contexts made it difficult to directly compare size and position of shape features belonging to different objects, and partly because the axes used throughout the representation were often not relevant to the problem. A far more useful aspect of shape for determining interaction is the form of the shape boundary.
All interaction between objects occurs on the boundaries of the interacting objects. This fact encouraged the development of a second shape representation which concentrated on simply making the object boundary explicit, rather than attempting to decompose the shape into a hierarchy of shape components.
This technique for qualitative description of shape boundaries starts by dividing the boundary into segments that are qualitatively homogeneous, e.g. a homogeneous segment of the boundary might be a simple line or a curve. Homogeneous segments are separated by qualitative discontinuities, referred to as junctions. The boundary of an object can be described by a circular list of alternating segments and junctions. This extended polygon boundary description has been used in other research, especially in vision (e.g. see Reference [20]), but not necessarily for qualitative shape description.
Useful information about object shape and possible object interaction can be stated directly in terms of these boundary elements. A boundary segment can be qualitatively described as either a line, a simple concave or convex curve, or a curve with points of inflection (a 'wiggle'). Junctions between segments can be described by the angle at which the segments join: a simple qualitative classification can include concave or convex junctions, which may be either acute, obtuse or right-angled.
Further sophistication is added to this shape representation by allowing different levels of detail to be superimposed in the boundary description, e.g. a boundary element may appear at a coarse level of detail to be a right angled junction, but at a fine level of detail it is actually a small radius curve. This information can be recorded by describing complex portions of the boundary at more than one level of detail. A spatial reasoning system can then select the level of detail appropriate for a given operation, e.g. a small radius might be irrelevant for almost all operations, and a coarser level of detail can be employed. The fine detail information would, however, be available when needed.
Shape representation using only the boundaries of an object means that there is no single feature in the shape description that can be used as a local reference for size comparisons (in the way that an axis can be used). This is not a great disadvantage, since object-local size description makes it difficult to compare sizes of interacting parts on different objects. A qualitative description technique which allows explicit size comparisons to be made wherever necessary is the partial ordering, as used by Simmons in his Commonsense Arithmetic[21].
The partial ordering classifies magnitudes by defining for any quantity another quantity in the ordering that is known to be larger, and another quantity that is known to be smaller. The accuracy with which a given quantity is known depends on how close together these bounding values are. This type of ordering can be used for the direct comparison of boundary element sizes, without requiring quantitative or absolute size information.
The lack of any definitive reference feature or shape axis in the boundary description also means that it is necessary to select elements on the boundary with respect to which the position of other objects can be described. A useful approach to this is to describe places where elements on the boundaries of different objects are in close proximity to each other. Points at which such a relationship should be recorded are selected using a proximity transform.
The proximity transform involves "expanding" the boundaries of all objects in a scene until they contact each other. Any point at which the expanded boundaries would meet is recorded as a proximity pair of two boundary elements. If the expansion of all boundaries takes place at the same rate, the order in which contacts occur can be used to represent the relative distances between proximity pairs. This ordering of proximity distance becomes the basis of a distance ordering for the whole scene, which includes the partial ordering of boundary segment sizes. The proximity transform used in this project to construct qualitative scene descriptions actually 'expands' along the boundary segments at the same time as it expands the boundaries themselves. This results in a complete Partial Distance Ordering of all distance and size information in the scene, that is used as the basis for spatial reasoning.
The qualitative extended polygon boundary shape
representation can be implemented in a quite straightforward manner.
This project employed the Lisp language, and created a circular list
of boundary elements for each shape using LEFT and
RIGHT properties for each element. A TYPE
property recorded whether each element was a JUNCTION or
SEGMENT, and SHAPE could be
CONVEX or CONCAVE, STRAIGHT,
CURVED, RIGHT angled, etc. as appropriate
for either a segment or junction. To achieve multiple levels of
detail, the LEFT and RIGHT properties were
lists, which were ordered from coarse to fine detail. The boundary
description was therefore a circular network, which could be traversed
at any level of detail, or at varying levels as required.
The partial distance ordering was implemented as a network of
equidistance lists, each of which referred to a number of
boundary segments or proximity distances that were the same size. Each
equidistance list was positioned in the ordering by a
LARGER and SMALLER property, each a pointer
to another equidistance list. One special equidistance list was the
CONTACT list. No size in the distance ordering could be
smaller than the contact list, and it had the special function of
recording where separate objects are in contact - contacts being
special cases of the proximity pair.
Two simple extensions would make this representation useful in a
wider range of problems, although they have not been implemented.
First, it would be possible to increase the amount of size information
by including order of magnitude comparison as well as simple relative
size comparison. This would enable techniques such as Raiman's
order of magnitude reasoning [22] to be
applied. Order of magnitude information could be simply superimposed
on the partial distance ordering by use of MUCH-LARGER,
MUCH-SMALLER and NEARLY-EQUAL relationships
in addition to the present LARGER and
SMALLER.
A second useful extension would be to include more discrimination
between angle sizes. At present, junction angles and curve angles have
only seven possible qualitative values (CONCAVE-ACUTE,
CONCAVE-RIGHT, CONCAVE-OBTUSE,
STRAIGHT, CONVEX-OBTUSE,
CONVEX-RIGHT and CONVEX-ACUTE). This could
be extended by the use of a partial ordering of angles. Qualitative
distinguished points, such as right angles, could be annotated as
special points in the ordering, in the same way as for the contact
list in the distance ordering.
Even without these extensions, the implementation described can be used to accomplish the spatial reasoning tasks described in the introduction. The way in which these are carried out is described below.
Methods used for solving two problems in two dimensional spatial reasoning are described here. A system for reasoning about sliding motion, the sliding system, was based on a qualitative shape representation using Axially Specified Subparts and Features (ASSF). In addition, a system for planning a path through free space between obstacles is described. The path planning system was based on a qualitative Extended Polygon Boundary (EPB) representation. It was in the course of the first implementation that the limitations of the ASSF representation became apparent, and it would be straightforward to reimplement the system described using EPB.
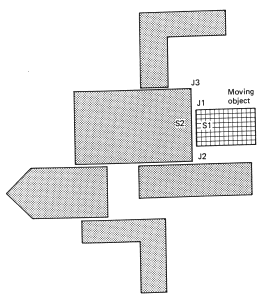
The sliding problem starts with an initial situation in which there are a number of stationary objects (which may or may not be in contact with each other), and one moving object. A typical initial situation is shown in Figure 1. The system must determine how many different contacts can occur between the moving and stationary objects when the moving object is constrained by the condition that it must always remain in contact with at least one of the stationary objects. The required solution is a list of possible contacts between surfaces on the moving object and on stationary objects.

Figure 1. Typical initial situation for the sliding problem
| State 1: | ...(S1 S2)(J1 S2)(J2 S2)(S2 J1 S1 J2)... |
| State 2: | ...(J1 J3)(S1 S2)(J2 S2)(J3 J1)(S2 S1 J2)... |
| State 3: | ...(S1 S2 J3)(J2 S2)(S2 S1 J2)(J3 Sl)... |
Figure 2. Portion of the solution set showing several contacts that can follow from the initial situation shown in Figure 1.
The most important piece of information about the scene is the description of all contacts between objects, since this set specifies the motion constraints that define sliding, and is also used to express the solution.
The spatial reasoning involved in solving this problem primarily requires the ability to recognize what kinds of surface can slide over each other, and what sort of transitions take place between different types of contact configuration as a result of sliding. Basic contact configurations include aligned straight edges, where vertices neighbouring the edges are in contact as well as the edges, overlapping straight edges, where one vertex on each object is in contact with the straight edge on the other, and contact of unequally sized edges, where two vertices and an edge on one object are in contact with one edge on the other.
These basic contact configurations all describe parallel edges. A more complex set of relationships defines contacts between various combinations of concave and convex vertices and curves. Angled meetings of straight edges always involve one convex vertex in contact with one edge. Convex curves can be in contact either with straight edges or with vertices, but not with a neighbouring edge and vertex. Concave curves cannot be directly in contact with straight edges, but only with vertices or convex curves, and so on.
Qualitative changes of state in possible sliding motion all involve transitions between the full set of these contact configurations. The reasoning system has access to a set of definitions which describe the possible transitions, and relates them to preconditions in arrangement of the boundary, e.g. a transition from an aligned edge to-edge contact directly to a curve-to-edge contact is not possible; it must be preceded by an overlapping edge-to-edge contact.
The basic component of the reasoning system determines the effect of sliding in a given direction (specified relative to the moving object as clockwise or anticlockwise), and updates the set of contacts for the scene to represent each new state. A high level search strategy must be superimposed to ensure that all possible state changes have been recorded, and to determine when the search is complete. A solution set of all sliding contacts can be compiled from the complete history of contact states that is maintained by the search algorithrm. A portion of the solution set, showing several contacts that can follow from the situation in Figure 1, is shown in Figure 2.
This system performs comparably to a human in simple spatial reasoning tasks, working from qualitative data. The representation elements required to achieve this include separation of curves, straight edges and vertices in two dimensional shape, discrimination between concave and convex, and between clockwise and anticlockwise, and relative description of angle and size. A number of features of the ASSF representation were not used here, although those features make the shape description sound more natural to a human. This program could equally well have used the EPB representation, while the program described below could not have used ASSF.
In the qualitative path planning problem, a moving object is surrounded by obstacles (see Figure 3). It must travel between these obstacles in order to reach free space on the outside. The initial state is therefore exactly specified, but the goal state is any position where movement is unconstrained. The solution is expressed as a series of qualitative movement instructions that will bring the moving object to the goal state.
The overall method used to find a solution can be expressed quite simply. The first step is to find a gap between the obstacles that are constraining motion (Figure 4a lists typical gaps found for the example in Figure 3). The second step is to confirm that the moving object can fit through this gap (producing analyses of fit as in Figure 4b), and the final step is to describe the motions that will move the object through the gap (motion specifications in Figure 4c). The second and third steps must interact, since fit depends on how the objects move through the gap.
There are two important spatial reasoning facilities that are
necessary to find a solution to this problem. First, it is necessary
to reason about distances other than those that have been explicitly
included in the partial distance ordering when the scene description
is constructed, e.g. fit may depend on the size of an object from
corner to corner, when the partial distance ordering has only
information about the size of individual boundary elements. In order
to allow reasoning about such distances, they must be included in the
partial ordering. Such values are a special type:
SYNTHETIC distances which have been determined by
reasoning, rather than from the proximity transform.
It is also necessary to reason about direction of motion. Some motion directions can be expressed precisely by a qualitative reasoning system, where the requirement might be, e.g. 'move vertex-A closer to vertex-B'.
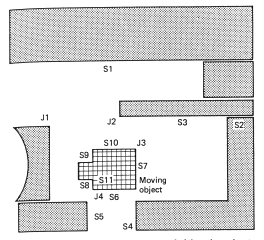
Figure 3. A moving object is surrounded by obstacles in the qualitative path planning problem
(a) Gaps: |
| (b) Fit: |
width forward from S6 = (synthetic (+ S6 S8)) (q < (synthetic (+ S6 S8)) (proximity (S5 S4))) FALSE - therefore no fit width forward left from S7 = (size S7) (q < (size S7) (proximity (S2 S3))) FALSE - therefore no fit width forward right from S9 = (size S7) (q < (size S7) (proximity (J1 S1))) TRUE - therefore may fit |
(c) Motion: |
|
Figure 4. Expressing the solution for the qualitative path planning problem: (a) typical gaps found for the example given in Figure 3; (b) producing analyses of fit; (c) motion specifications.
Other directions must be expressed in imprecise terms, such as 'move forward-and-to-the-left'. In these circumstances, directional reasoning must be capable of graceful degradation when directions are not known precisely. The system can allow for this by annotating directions if they are 'vague' or 'exact', and preferring exact results from deductions when possible. A similar preference is given in distance reasoning for values in the partial distance ordering which are more closely constrained.
[There was an extra paragraph at this point in the published paper. As far as I can tell, it was included as the result of a proof-reading error, so I have removed it.]
The first step of checking a gap to see if the moving object will fit through it is to find the narrowest extent of the gap. The narrowest extent can be determined directly from the partial distance ordering. In the present version of the system, fit is caclulated on a simply linear basis, since motion does not include rotation of the moving object around obstacles.
The fit of the moving object through the gap depends secondly on the 'width' of the object in the direction of travel. This must be determined from boundary description information by selecting candidates for the widest extremities on the moving object that might interfere in the direction of motion chosen for a given gap. The distance between these extremities must then be estimated.
This estimated distance is expressed as a synthetic value in the partial distance ordering, with no initial constraints on the range of values it may take. The system then applies a variety of techniques to reduce the range of possible values for the distance estimate. These techniques include a method called qualitative trigonometry, described by Blackwell[23].
Once the effective width for a given direction of motion has been determined as closely as possible, it can be directly compared to the narrowest extent of the proposed gap. If it will fit, the motion direction used for deriving travelling width can be confirmed, and the system can check for possible obstacles on the path to the gap. If there are pairs of obstacles which are close together (relative to the size of the moving object), they can be negotiated by another iteration of the gap finding method. If single obstacles obstruct the path, they can be negotiated using a straightforward adaptation of the techniques for reasoning about sliding.
This path planning method appears similar to the way that humans deal with very simple path planning situations (those that can be immediately assessed by eye, with no measurement required). The system is able to recognize cases in which no path is available, and also cases in which a clear path is present. There are, however, many situations in which it would be unable to make a firm conclusion. In these cases, the graceful degradation facilities will still allow it to rank possible paths in order of likelihood, so that they can be evaluated by a formal geometric system, by measurement, or by trial and error (the most common human approach)!
The methods described here for qualitative space and shape representation, and for qualitative reasoning about motion, can be evaluated from two possible points of view: first, as a means for adding general spatial reasoning abilities to the repertoire of techniques in qualitative physics; and second, as a new method for enhancing performance in established spatial reasoning domains, especially robotics. This conclusion is therefore divided into two sections, to consider the application of these methods in each context.
Spatial reasoning was identified by Hayes as a major concern for naive physics, and it is also recognized as important to qualitative physics. Qualitative physics work has included a number of systems that operate on problems with a spatial component, but it has concentrated on questions of process, reducing spatial information to simple connectivity between devices or regions of space. In mechanical domains, conventional geometric techniques for determining possible motion have been used to 'preprocess' spatial information for the qualitative system.
The methods described in this paper use purely qualitative information, and reason about motion in qualitative terms such as those used by people. The lack of any numerical problem description means that there are some problems which cannot be solved using these methods, since some infomation is lost in the construction of the qualitative description. The test of a qualitative representation is not, however, whether it retains complete information, but whether it provides an adequate description of the structure of a problem.
The extended polygon boundary/partial distance ordering representation could be used as a spatial foundation for several qualitative physics systems which have previously used numerical techniques at the spatial level. These include de Kleer's roller coaster problem, Forbus's bouncing ball, and the two dimensional mechanism problems.
The methods described here do not constitute a full qualitative physics system, because they do not presently include any explicit description of process or causation. A complete qualitative spatial reasoning system capable of human-like reasoning would have to take account of externally imposed directions imposed by forces such as gravity, and would also require an explicit description of motion, rather than the simple sequence of global state descriptions currently used.
The qualitative techniques described here are less powerful in many situations than the geometric techniques currently used for robotic guidance, since they have no way of expressing the precise positional information required by robots. What they provide for robot applications is a basis for reasoning about space and motion at a level close to human reasoning.
The data input to this system is similar to human perception of a two dimensional scene, in that it describes relative position and contact, together with general shape properties at variable levels of resolution. The expression of intermediate conclusions about motion or position is also similar to human concepts, e.g. we would often use no terms more precise than 'move forward and to the left'.
This can be an advantage for robot reasoning systems where high level planning is being carried out at the level that humans would normally be involved. In an activity such as task-level programming, the robot may have access to motion "strategies" which include all the quantitative information necessary to perform a given task, while selection of these strategies can be carried out on a purely qualitative basis.
The second advantage of these methods over numeric techniques is the built-in graceful degradation that results from working with qualitative data. The system described for path planning is able to operate quite satisfactorily when data is missing, or even sometimes when it is wrong. The system is able to recognize when the available data is insufficient to complete the required task, and it is then able to ask for more data, or perform an experiment; in either case, new information can be simply added to the partial distance ordering (the scene description does not have to be reconstructed), and reasoning can proceed.
The ability to work where there is imprecise or unspecified data is also essential in design work. High level robot programming operates in exactly this kind of environment, and qualitative spatial reasoning could form the basis of a robot programmer's advisor, which can evaluate estimated information, point out conflicts, and assist with similar design tasks.
The representation and reasoning strategies described in this paper provide a basis for purely qualitative spatial reasoning. The extended polygon boundary/partial distance ordering representation supports human-like performance in two simple spatial reasoning tasks. The representation provides a foundation for qualitative spatial reasoning that extends the spatial component of current qualitative physics systems. It also provides spatial reasoning mechanisms that could provide a human interface for high level robot programming.
The author is indebted to Dr Peter Andreae, who has supervised this research project, providing invaluable assistance and criticism, and to PROGENI, who have provided financial support during its course.
1. Pugh, A. (1982). Second generation robotics. Proceedings of the 12th International Symposium on Industrial Robots.
2. Jacobsen, S. C., Wood, J. E., Knutti, D. F. and Biggers, K. B. (1984). The Utah/MIT dextrous hand: work in progress. International Journal of Robotics Research 3(4).
3. Dario, P. and de Rossi, D. (1985). Tactile sensors and the gripping challenge. IEEE Spectrum, August 1985.
4. Wong, E. K. and Fu, K. S. (1986). A hierarchical orthogonal space approach to three-dimensional path planning. IEEE Robotics & Automation 2(1), 42-52.
5. Lozano-Perez, T. (1982). Robot programming. AI Memo No 698a, MIT AI Laboratory.
6. Popplestone, R. J., Ambler, A. P. and Bellos, I. M. (1980). An interpreter for a language for describing assemblies. Artificial Intelligence 14(1), 79-107.
7. Ambler, A. P., Barrow, H. G., Brown, C. M., Burstall, R. M. and Popplestone, R J. (1975). A versatile system for computer controlled assembly. Artificial Intelligence 6(2).
8. Kim, Y. C. and Aggarwal, J. K. (1986). Rectangular paralleliped coding: a volumetric representation of three dimensional objects. IEEE Robotics and Automation 2(3).
9. Lozano-Perez, T. (1979). A language for automated mechanical assembly. In P.H. Winston and R.H. Brown. (Eds) Artificial Intelligence: an MIT Perspective MIT Press.
10. Cronshaw, A. G. (1982). Automatic chocolate decoration by robot vision. Proceedings of the 12th International Symposium on Industrial Robots.
11. Trevylan, J. P., Kovesi, P. D. and Ong, M. C. H. (1982). Techniques for surface representation and adaptation in automated sheep shearing. Proceedings of the 12th International Symposium on Industrial Robots.
12. Brady, M. and Asada, H. (1984). Smoothed local symmetries and their implementation. AI Memo No 757 MIT AI Laboratory.
13. Lieberman, L. I. and Wesley, M. A. (1977). AUTOPASS: an automatic programming system for computer controlled mechanical assembly. IBM Journal of Research & Development 21(4).
14. de Kleer, J. (1977). Multiple representations of knowledge in a mechanics problem solver. Proceedings of the International Joint Conference on Artificial Intelligence, 299-304.
15. Hayes, P. J. (1978). The naive physics manifesto. In D. Michie (Ed.) Expert Systems in the Microelectronic Age. Edinburgh University Press.
16. Bobrow, D. G. (Ed.) (1984). Qualitative Reasoning About Physical Systems. Netherlands: Elsevier.
17. Joskowicz, L. (1987). Shape and function in mechanical devices. Proceedings of the National Conference on AI (AAAI'87), 611-615.
18. Stanfill, C. (1983). The decomposition of a large domain: reasoning about machines. Proceedings of the National Conference on AI (AAAI'83), 387-390.
19. Forbus, K. D., Nielsen, P. and Faltings, B. (1987). Qualitative Kinematics: A Framework. Technical Report UIUCDCS-R87-1352, Department of Computer Science, University of Illinois at UrbanaChampaign.
20. Mackerras, P. (1987). Formulating and testing simple boundary hypotheses in textured images. Australian Joint Conference on Artificial Intelligence (AI'87), 266-278.
21. Simmons, R. (1986). "Common sense" arithmetic reasoning. Proceedings of the National Conference on Artificial Intelligence (AAAI'86), 118-124.
22. Raiman, O. (1986). Order of magnitude reasoning. Proceedings of the National Conference on Artificial Intelligence (AAAI'86), 100-104.
23. Blackwell, A. F. (1988). Qualitative geometric reasoning using a partial distance ordering. In J.S. Gero. and R.Stanton (Eds) Artificial Intelligence Developments and Applications. North-Holland, Netherlands, 217-229.