Tick 1. Econophysics simulator

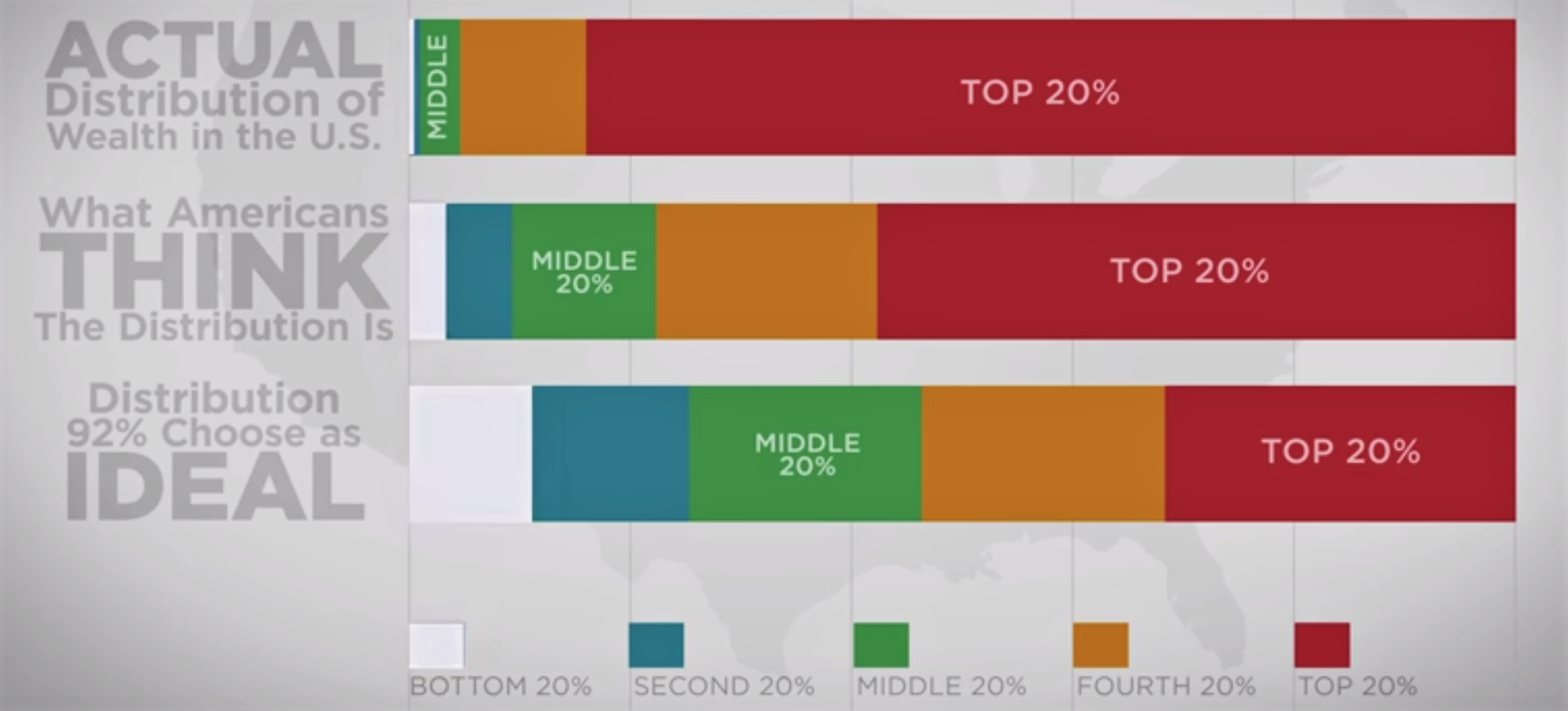
Economic inequality is one of the defining social issues of our age. Yet we have a poor grasp of the scale of inequality, as described in Scientific American and nicely shown in this video:

How does inequality arise? Is it an inevitable outcome of liberal economics, and if so how can it be mitigated by economic policy? These questions have been studied by economists and more recently by physicists. In this assignment you will investigate a simple "econophysics" model of inequality.

Here is a simple model. There are $N$ individuals in the population, each with an initial wealth of £1. Every timestep, we randomly group them into $N/2$ pairs. (Assume $N$ is even.) For every pair, we simulate an economic exchange, as follows. Let the two paired individuals have wealth $v$ and $w$, and update their wealth according to $$ v_{\text{new}} = R(v+w), \quad w_{\text{new}} = (1-R)(v+w) $$ where $R$ is a random number in $[0,1]$, chosen independently for every pair and at every timestep. This model is loosely inspired by the physics of gases, in which two gas molecules exchange a random amount of energy whenever they collide, and so it's called the Kinetic Exchange model.

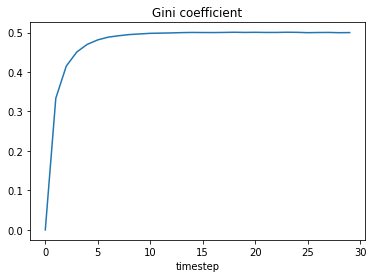
We can measure inequality with the Gini coefficient, $$ G = 2\frac{\sum_{i=1}^N i\, w_{(i)}}{N \sum_i w_{(i)}} - \Big(1 + \frac{1}{N}\Bigr) $$ where $w_{(1)}$ is the smallest value, $w_{(2)}$ the second smallest etc. If everyone has the same wealth then $G=0$; if one person has all the wealth then $G=1-1/N$.

Extension. In the kinetic exchange model, the poorest and the richest might swap places after just one transaction, which isn't a great fit for real economics. There's an alternative model for exchange, that will be used in Tick 3, which we might call the "Value Transfer Model". As before, suppose that two individuals with wealth $v$ and $w$ respectively are paired, but now let their wealth be updated by $$ v_{\text{new}} = v + R \min(v,w), \quad w_{\text{new}} = w - R \min(v,w) $$ where $R$ is now a random number in $[-1,1]$, chosen independently for every pair at every timestep. The idea is that each party to the exchange puts up a certain amount of money, but no more than they can afford.

Questions

Use these autograder settings:

import ucamcl
GRADER = ucamcl.autograder('https://markmy.solutions', course='scicomp_2022').subsection('tick1')

This assignment tests your vectorized thinking. You will be asked to run simulations on a population of hundreds of thousands of individuals, over many timesteps. YOUR CODE MUST USE NUMPY VECTORIZED OPERATIONS rather than iterating over the population. You may use Python iteration over timesteps.

Question 1. The model needs us to randomly group the population into $N/2$ pairs. We can do this by randomly permuting the vector $[0,...,N-1]$, letting the vector m1 consist of the first $N/2$ integers and m2 consist of the rest, and interpreting it as "m1[i] is paired with m2[i]".

Write a function pairs(N) that returns a tuple (m1,m2) where m1 and m2 are both vectors of length $N/2$ as described above. For example, if you run pairs(6), you might get the output

(array[3, 0, 1]), array([2, 4, 5]))

To submit your answer,

q = GRADER.fetch_question('q1')
m1,m2 = pairs(q.n)
ans = {'n': len(np.unique(np.concatenate([m1,m2]))), 's': np.std(np.abs(m1-m2))}
GRADER.submit_answer(q, ans)

Question 2. Write a function kinetic_exchange(v,w) which takes two wealth vectors v and w, each of length $N/2$, and returns a tuple (vnew, wnew) with two new vectors, according to the kinetic exchange model. To submit your answer,

q = GRADER.fetch_question('q2')
v,w = np.linspace(1,5,q.n), np.linspace(1,2,q.n)**q.p
vnew,wnew = kinetic_exchange(v,w)
ans = {'m1': np.mean(vnew), 's2': np.std(wnew)}
GRADER.submit_answer(q, ans)

Question 3. Write a function gini(w) which takes a vector w and returns the Gini coefficient. To submit your answer,

q = GRADER.fetch_question('q3')
w = np.linspace(0,1,q.n)**q.p
g = gini(w)
GRADER.submit_answer(q, {'g': g})

Question 4. Write a function sim(N, T) which runs the kinetic exchange model on a population of $N$ individuals for $T$ timesteps. It should return a pair (w, gs) where w is the wealth vector after $T$ timesteps, and gs is a length $T$ vector where gs[i] is the Gini coefficient at timestep $i$. To submit your answer,

q = GRADER.fetch_question('q4')
w,gs = sim(q.n, q.t)
ans = {'gm': np.mean(gs[int(q.t/2):]), 'gs': np.std(gs[int(q.t/2):]), 'ws': np.std(w)}
GRADER.submit_answer(q, ans)

Question 5. Simulate a population of 500,000 over 30 iterations. Plot the Gini coefficient as a function of timestep. To be precise, if $w_t$ is the wealth vector after $t$ timesteps then you should plot $\textsf{gini}(w_t)$ on the $y$-axis and $t$ on the $x$-axis.

Your plot should look something like this. If it doesn't, there's likely a big which will hinder you in later questions. You don't have to submit your plot.