Example Problem Set 8

Consider the family of 1D Gabor wavelets, parameterized for location x₀, size 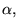$\alpha,$ and frequency 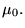$\mu_{0}.$ Their functional form is:

$$f(x) = e^{-i\mu_{0}x} e^{-(x-x_{0})^{2}/\alpha^{2}}$$

and their Fourier Transform is:

$$F(\mu) = e^{-ix_{0}\mu} e^{-(\mu-\mu_{0})^{2}\alpha^{2}}$$

1.

Are such families of functions ``self-Fourier?" Why or why not?

2.

Explain the dualities of: (i) modulation and shifting; and (ii) similarity (reciprocal scaling), in terms of the behaviour of the parameters in the expressions above for f(x) and $F(\mu)$.

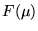3.

What can you say about the Fourier transform of the sum of any two Gabor wavelets?

4.

What can you say about the Fourier transform of the product of any two Gabor wavelets, and why?

5.

What is the Fourier transform of f⁽ⁿ⁾(x), the 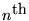$n^{\mbox{th}}$-derivative of a Gabor wavelet?

6.

Show that the set of all Gabor wavelets is closed under convolution: i.e., that the convolution of any two Gabor wavelets is itself a single Gabor wavelet.