


Next: Example Problem Set 5
Up: Continuous Mathematics
Previous: Example Problem Set 3
Suppose that some continuous function f(x) has Fourier Transform 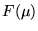 .
Now consider the consequences in the Fourier domain of each of the following
operations upon f(x):
.
Now consider the consequences in the Fourier domain of each of the following
operations upon f(x):
- 1.
- What will be the Fourier Transform of the mth derivative
of f(x) with respect to x:
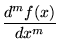 ?
?
- 2.
- What will be the Fourier Transform after
shifting f(x) by a distance
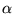 :
:
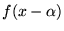 ?
?
- 3.
- What will be the Fourier Transform after
dilating f(x) by a factor
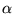 :
:
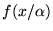 ?
?
- 4.
- Suppose that f(x) is convolved with another function g(x)whose Fourier Transform is
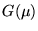 .
What will be the Fourier Transform
.
What will be the Fourier Transform
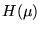 of the convolution result h(x) where
of the convolution result h(x) where
- 5.
- Suppose now that a two-dimensional continuous function f(x,y) has a 2D
Fourier Transform
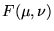 .
Define the Laplacian operator
.
Define the Laplacian operator
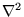 and express the 2D Fourier Transform of
and express the 2D Fourier Transform of
 .
.
Neil Dodgson
2000-10-20
![]() .
Now consider the consequences in the Fourier domain of each of the following
operations upon f(x):
.
Now consider the consequences in the Fourier domain of each of the following
operations upon f(x):
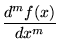 ?
?