Big-O and $\Theta$ notation

All the while in Computer Science we are concerned with how long things are going to take. It is almost always necessary to make a few simplifying assumptions before starting of cost estimation, and for algorithms the ones most commonly used are:

1.

We only worry about the worst possible amount of time that some activity could take. The fact that sometimes our problems get solved a lot faster than that is nice, but the worst case is the one that is most important to worry about.

2.

We do not know what brand of computer we are using, so rather than measuring absolute computing times we will look at rates of growth as our computer is used to solve larger and larger problems of the same sort. Often there will be a single simple number that can be used to characterise the size of a problem, and the idea is to express computing times as functions of this parameter. If the parameter is called n and the growth rate is f(n) then constant multipliers will be ignored, so 100000 f(n) and 0.000001 f(n) will both be considered equivalent to just f(n).

3.

Any finite number of exceptions to a cost estimate are unimportant so long as the estimate is valid for all large enough values of n.

4.

We do not restrict ourselves to just reasonable values of n or apply any other reality checks. Cost estimation will be carried through as an abstract mathematical activity.

Despite the severity of all these limitations cost estimation for algorithms has proved very useful, and almost always the indications it gives relate closely to the practical behaviour people observe when they write and run programs.

The notations bit-O and $\Theta$ are used as short-hand for some of the above cautions.

A function f(n) is said to be O(g(n)) if there are constants k and Nsuch that f(n) < k g(n) whenever n > N.

A function f(n) is said to be $\Theta(g(n))$ if there are constants k₁, k₂ and N such that k₁g(n) < f(n) < k₂g(n) whenever n > N.

Note that neither notation says anything about f(n) being a computing time estimate, even though that will be a common use. Big-O just provides an upper bound to say that f(n) is less than something, while $\Theta$is much stronger, and indicates that eventually f and g agree within a constant factor. Here are a few examples that may help explain:

$$\begin{eqnarray*}sin(n) & = & O(1) \\ sin(n) & \neq & \Theta(1) \\ 200+sin(n) ... ... = & O(n) \\ n^{100} & = & O(2^{n}) \\ 1+100/n & = & \Theta(1) \end{eqnarray*}$$

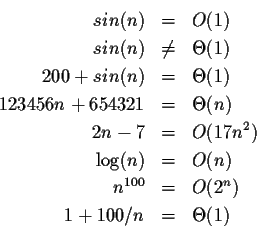
Various important computer procedures have costs that grow as $O(n \log(n))$. In the proofs of this the logarithm will often come out as ones to base 2, but observe that $\log_{2}(n) = \Theta(\log_{10}(n))$ [indeed a stronger statement could be made--the ratio between them is utterly fixed], so with Big-O or $\Theta$ notation there is no need to specify the base of logarithms--all versions are equally valid.