

Next: Relations and Graphs and
Up: No Title
Previous: Proofs and Induction
Very many computer data structures are best reasoned about using things
called ``sets''. For the purpose of this course a set is collection
of things, and is written by listing the members of the set inside
curly brackets.. So for instance the set whose members are the first five
whole numbers might be written {0,1,2,3,4}. It is perfectly possible
to have a set with no members at all, and it is then (obviously) written
as {}, and known as the empty set. There are a number of rules about
sets and a collection of things you are allowed to do with them:
- The members of a set should not be thought of as being there in
an particular order, even though when you write down a representation of
a set you have to list them somehow. So for instance {1,2,3},
{3,1,2} and {2,1,3} are all just different ways of writing down the
same set.
- Any particular object can either be in a set or not. The consequence
of this is that when you list the members of a set you should never see
any duplicates. It is not possible for an object to be a member of a set
twice or more times, so {1,1,1,2,2,3} is not a valid things to write.
- As well as having the null set {} it is (of course) quite
proper to have sets that have a single member. Set members can be
arbitrary things, including other sets. Thus we can have the number 1,
and the sets {1}, {{1}}, {{{1}}}. These are all quite
different things. For instance the set {{}, {{}}} is a set with
two members (one of which is the empty set, the other is a set whose sole
member is the empty set).
- It is quite common to use upper case letters to stand for
sets and lower case ones for the items that may be members of those
sets. The notation
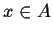 is used to indicate set membership. x is
an object and A is a set. Eg
is used to indicate set membership. x is
an object and A is a set. Eg
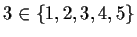 is true. The notation
is true. The notation
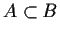 is used to indicate that A is a subset of B, ie it has
as its members some selection from the members of B. Eg
is used to indicate that A is a subset of B, ie it has
as its members some selection from the members of B. Eg
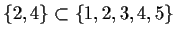 .
.
- The notation
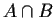 is a set whose members are just those things
that are present in both A and B (the intersection), while
is a set whose members are just those things
that are present in both A and B (the intersection), while
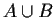 has all the members that are in either (or both) A and B(the union).
has all the members that are in either (or both) A and B(the union).
- The exact rules for the treatment of very infinite sets are not needed
in this course, but informal notation will be used to describe simple
cases, such as the integers
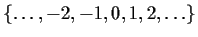 .
The
expression
.
The
expression
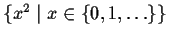 stands for
stands for
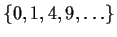 .
.
- Given a finite set you can find out how many members it has. The
number is known as the cardinality of the set (or more simply as its
size), and is sometime written |A| as in
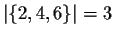 .
.
An ordered pair is just a pair of things grouped together where
(unlike the situation with sets) the ordering of the two items does match.
Such pairs will be written with parentheses as in (1,2) rather than
curly brackets. This idea will be extended to ordered triples, quadruples,
5-tuples and so on, and in general n-tuples. The objects in an n-tuple
do not need to be all of the same sort. Eg here is a 4-tuple
(1, "string", {{}, {22}}, x}
where the third member of the 4-tuple is a set.
Given one or more sets there are ways of constructing bigger sets out of
them. The cartesian product of two sets A and B is the set of ordered
pairs (a,b) with 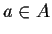 and
and 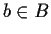 .
Eg
.
Eg
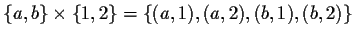 .
The powerset of a set A is the collection
of all subsets of A. Eg. powerset(
.
The powerset of a set A is the collection
of all subsets of A. Eg. powerset(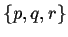 )
)
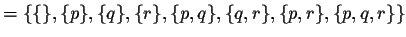
You might like to convince yourself that
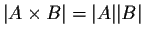 and
|powerset
(A)| = 2|A|. For the powerset example try induction on
the size of the set.
and
|powerset
(A)| = 2|A|. For the powerset example try induction on
the size of the set.
Given a set X , a relation is some property that may or may not hold
between one member of X and another.
For instance if attention is restricted to sets of numbers then the
operator ``<'' for ``is less than'' is
a valid relation, as would be ``='' for equality. Sometimes people will
want to use a general name, say R for an unspecified relation, and then
rather than something concrete like x=y they will write xRy to show
that x relates to y under R.
Relations are not only things that arise with numbers. In a family tree (or
many computer data structures you will come across later) the relation ``is
an ancestor of'' can be relevant. Given a set of people one could
specify the relationship ``likes'' (useful for a computer-based
system for arranging seating plans at large dinners?). A final example
is the ``is married to'' relation.
Relations can have different properties, and the examples given above can
illustrate some of the important ones:
- Reflexive:
- Given any member of the set, x say, does the relation
hold true between x and itself. For = it does, for < and
``is married to'' it does
not and for ``likes'' the status is unclear to me. Relations that
have this property are known as reflexive. From any (possibly non-reflexive)
relation you can derive something called the reflexive closure by forcing
each item x to relate to itself but otherwise leaving conditions unchanged.
- Symmetric:
- Of the examples given here, = and ``is married to'' have
the property that if (x,y) relate then (y,x) do too. This makes them
symmetric, while < is clearly not. Again the extent to which ``likes''
is a symmetric relation on any particular set is an interesting social
consideration. The reflexive closure of a relation extends a relation
to force symmetry. Eg the symmetric closure of < is
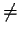 .
.
- Transitive:
- If x=y and y=z then we may deduce that x=z.
Similarly for <, and these relations are, on account of this, known as
transitive. There is such a thing as a transitive closure, which is
discussed in the next section.


Next: Relations and Graphs and
Up: No Title
Previous: Proofs and Induction
Alan Mycroft
1998-10-05
![]() and
and ![]() .
Eg
.
Eg
![]() .
The powerset of a set A is the collection
of all subsets of A. Eg. powerset(
.
The powerset of a set A is the collection
of all subsets of A. Eg. powerset(![]() )
)
![]()
![]() and
|powerset
(A)| = 2|A|. For the powerset example try induction on
the size of the set.
and
|powerset
(A)| = 2|A|. For the powerset example try induction on
the size of the set.