Replacing Queues With Delay Estimates

This slide/section not lectured in 2017/18.

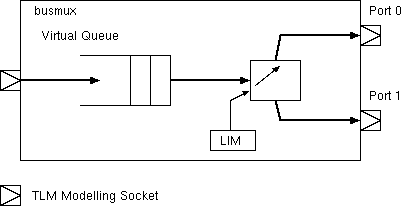
With a virtual queue, although the TLM call passes through the bus/NoC model without suffering delay or experiencing the contention or queuing of the real system, we can add on an appropriate estimated amount.

Delay estimates can be based on dynamic measurements of utilisation at the contention point, in terms of transactions per millisecond and a suitable formula, such as 1/(1-p) that models the queuing delay in terms of the utilisation.

  // A simple bus demultiplexor: forwards transaction to one of two destinations:
  busmux::write(u32_t A, u32_t D, sc_time &delay)
  {
     // Do actual work
     if (A >= LIM) port1.write(A-LIM, D, delay) else port0.write(A, D, delay);

     // Measure utilisation (time for the last 100 transactions) 
     if (++opcount == 100)
     {  sc_time delta = sc_time_stamp() - last_measure_time;
        local_processing_delay = delay_formula(delta, opcount); // e.g. 1 + 1/(1-p) nanoseconds
        logging.log(100, delta); // record utilisation
        
        last_measure_time = sc_time_stamp();
        opcount = 0;
     }

     // Add estimated (virtual) queuing penalty
     delay += local_processing_delay;
  }

In the above, a delay formula function knows how many bus cycles per unit time can be handled and hence can compute and record the utilisation and queuing delays.

The value `p' is the utilisation in the range 0 to 1. From queuing theory, with random arrivals, the queuing delay goes to infinity following a 1/(1-p) response as p approaches unity. For uniform arrival and service times, the queuing delay goes sharply to infinity at unity.