



Next: Transactor Synthesis
Up: SPL Orangepath H2 Language
Previous: Joining Automata Synthesis
Index
SSMG Refinement Algorithm
H2 is a vehicle for exploring various refinement algorithms.
In [#!ESL_Flip!#], it is proposed that all interfaces are constructed
using a combination of elemental interface paradigms and that any
description or implementation of an interface can be processed to
be represented in this way. The processing is a form of parsing
that generated a so-called interface transform. Once an interface is
represented this way, it can be render in a variety of detailed
output styles.
The default refinement algorithm uses a depth-first search and has
exponential cost in the worst case. A SAT-based algorithm was also
explored in the paper [#!Greaves_SAT!#], but is disabled in the tool
by default.
The refinement algorithm must first find a subset of the rules and
variables that are possibly needed in the target machine. The
following steps achieve this.
- Identify, from the compiler command line, the top-level target
variables that are to be driven by the target machine, thereby creating
a first target variable set, thenceforth known as the current target
variable set. Create an empty set of rules called the current rule
set.
- Identify any executable rules that drive variables in the target
variable set, or their past or future values, or assertion
rules that refer to them or their past or future values. Add these
safety and executable rules to the current rule set.
- If any variables occur in the current rule set that are not
external inputs and are not members of the current target variable
set, add them to the target variable set and go back to previous step.
The refinement algorithm then proceeds to generate further executable
rules from the assertion rules and to fill in concrete values for the
parameters and values of (?) encountered, thereby generating a
deterministic target machine.
The refinement algorithm uses a CNF/clause representation
of the design and is based around a built-in SAT solver.
- The safety assertions are all first converted into
a conjunctive-normal form and held on a safety clause list.
- For any executable rule that assigns a value to the next state of any
variable,
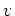 , all occurrences of
, all occurrences of 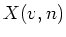 where
where 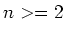 are substituted for
using that executable rule.
are substituted for
using that executable rule.
- For all values of all external inputs, subject to plant
constraints, the executable rules are examined for consistency and any
parameter values or non-det transitions that would make the executable
rules inconsistent are noted. Where only one possible value for a
parameter exists, the parameter is substituted out with that value,
otherwise the constraints are added as additional clauses to the
safety clause list.
- If the safety clause list is non-empty, a clause with a minimal
number of un-driven variables in its support is removed and converted
to an executable rule where one of the variables is driven by a LUT
function of all inputs and driven variables where the LUT contains
fresh parameters. Go back to previous step.
- When the safety clause list is empty, select a setting of all
parameters in the executable rules that creates a finite state machine
that satisfies all the liveness assertion rules. If none can be
found, then backtrack to the previous step and select a different free
variable of a safety clause to be driven by a LUT.
- Partition the resulting machine into hardware and software
components and output.
This algorithm does not reflect the sequencing constraints of the plant...
cf. Take all at once and SAT solve!




Next: Transactor Synthesis
Up: SPL Orangepath H2 Language
Previous: Joining Automata Synthesis
Index
David Greaves
2009-08-20