Discrete Mathematics

Lecturer: Dr P. Robinson

No. of lectures: 16 (Continued into Lent Term)

This course is a prerequisite for Introduction to Security (Part IB), Artificial Intelligence I (Part IB), Information Theory and Coding (Part II), Security (Part II).

Aims

This course will develop the idea of formal proof by way of examples involving simple objects such as integers and sets. The material enables academic study of Computer Science and will be promoted with examples from cryptography and the analysis of algorithms.

Lectures

Part A. Integers

• Proof. Deduction, contradiction. Integers, mathematical induction. [2 lectures]

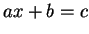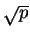• Factors. Division: highest common factors and least common multiples. Euclid's algorithm: solution in integers of $ax+b =c$, the complexity of Euclid's algorithm. Euclid's proof of the infinity of primes. Existence and uniqueness of prime factorisation. Irrationality of $\sqrt{p}$. [3 lectures]

• Modular arithmetic. Congruences. Units modulo m, Euler's totient function. Chinese remainder theorem. Wilson's theorem. The Fermat-Euler theorems, testing for primes. Public key cryptography, Diffie-Hellman and RSA. [3 lectures]

Part B. Sets, functions and relations.

• Sets, subsets and Boolean operations. Partitions. Boolean logic. [2 lectures]

• Binary relations. Composition of relations. Equivalence relations and quotients of sets. Closures and Warshall's algorithm. Partial orders and total orders. Hasse diagrams. Well-founded relations and well ordering. Well-founded induction. [3 lectures]

• Functions. Injective, surjective and bijective functions. Numbers of such functions between sets. Sorting. The Schröder-Bernstein theorem. Countability. A countable union of countable sets is countable. The uncountability of R. Existence of transcendental numbers. [3 lectures]

Objectives

On completing the course, students should be able to

• write a clear statement of a problem as a theorem in mathematical notation; prove and disprove assertions using a variety of techniques

• describe, analyse and use Euclid's algorithm; explain and apply prime factorisation

• perform calculations with modular arithmetic; use number theory to explain public key cryptography

• analyse problems using set theory; formulate statements using boolean logic

• recognise relations and discuss their properties; describe and analyse Warshall's algorithm

• state, prove and apply the Schröder-Bernstein theorem; distinguish countable and uncountable sets

Recommended books

* Humphreys, J.F. & Prest, M.Y. (1989). Numbers, groups and codes. Cambridge University Press.
* Rosen, K.H. (1999). Discrete mathematics and its applications. McGraw-Hill (4th ed.).

Biggs, N.L. (1989). Discrete mathematics. Oxford University Press.
Conway, J.H. & Guy, R.K. (1996). The book of numbers. Springer-Verlag.
Davenport, H. (1992). The higher arithmetic. Cambridge University Press (6th ed.).
Giblin, P. (1993). Primes and programming. Cambridge University Press.
Graham, R.L., Knuth, D.E. & Patashnik, O. (1994). Concrete mathematics. Addison-Wesley (2nd ed.).
Mattson, H.F. Jr (1993). Discrete mathematics. Wiley.
Nissanke, N. (1999). Introductory logic and sets for computer scientists. Addison-Wesley.
Pólya, G. (1980). How to solve it. Penguin.