Fig. 2. Messages of 1024 sections, 1 million trials, log scales
Richard Clayton and George Danezis
University of Cambridge, Computer Laboratory, Gates Building, JJ Thompson Avenue, Cambridge CB3 0FD, United Kingdom{ richard.clayton, george.danezis }@cl.cam.ac.uk
Abstract. We present the design and rationale of a practical system for passing confidential messages. The mechanism is an adaptation of Rivest's "chaffing and winnowing", which has the legal advantage of using authentication keys to provide privacy. We identify a weakness in Rivest's particular choice of his "package transform" as an "all-or-nothing" element within his scheme. We extend the basic system to allow the passing of several messages concurrently. Only some of these messages need be divulged under legal duress, the other messages will be plausibly deniable. We show how this system may have some resilience to the type of legal attack inherent in the UK's Regulation of Investigatory Powers (RIP) Act.
We present a system called "Chaffinch" for passing confidential messages using shared secret keys. The basic mechanism is Ron Rivest's "chaffing and winnowing" [10], which uses authentication primitives to provide confidentiality.
The Chaffinch system allows several further messages to be steganographically concealed behind the main message. This allows cover traffic to be divulged to any authorities who wish to inspect the confidential information, without compromising the hidden material. The system is evaluated not only in terms of the traditional threat to confidentiality, eavesdroppers with significant computing power, but also in terms of its interaction with the UK's Regulation of Investigatory Powers (RIP) Act [13], one of the first laws to attempt to engage with cryptography.
Section 2 of this paper discusses the background to "chaffing and winnowing". In particular, we identify a weakness in Rivest's suggestion that his "package transform" should be used as an "all-or-nothing transform" on a message. This section also provides an overview of the relevant parts of the RIP Act.
Section 3 provides a high-level description of the Chaffinch design. Section 4 covers a number of detailed design decisions that have been incorporated into the Chaffinch system. Finally, Section 5 covers the issues relating to secret keys and how best to manage the keys associated with Chaffinch communications.
Chaffing and winnowing was proposed by Rivest [10] as a way of providing confidentiality using only authentication primitives. In the basic scheme, a message is split into many equal sized packets and a valid MAC is appended to each. Some other random packets are also generated, but further random values are associated with them instead of correctly calculated MACs. The two sets of packets are intermingled and transmitted to the receiver. Anyone who holds the authentication key for the MAC values can recognise the good packets and distinguish them from the random material. Anyone else eavesdropping upon the data stream will be unable to determine which of the possible selection of packets will reveal the message. Rivest called the random packets "chaff" and the process of separating the true message "winnowing", by analogy with the harvesting task of separating the wheat from the chaff.
There is an obvious attack on this simple scheme, whereby an eavesdropper could select packets from the data stream based on the likelihood that they fit well with the packets already selected. There is also an obvious difficulty in sending chunks of information in the clear since natural language text can be easily distinguished from random material. These attacks are not applicable where single bits are sent -- but this is hugely inefficient if a very large MAC accompanies each bit. Rivest therefore proposed the use of his "package transform" [11] to produce a "packed message" with the two desirable properties that it was not practical to unpack it without having the whole message available and secondly that it would be statistically indistinguishable from random noise.
Rivest also pointed out that the "chaffing" operation of adding the random noise does not require knowledge of the MAC key and can even be performed by a third party, thus reinforcing the case that this system is not an encryption system in the usual sense of the word.
The basic idea was extended in two ways relevant to this work. Firstly, Rivest observed that the wheat of one participant might be used as the chaff for another. If two valid streams of packets are multiplexed together then the recipients will automatically discard the packets that they cannot authenticate and be left with the messages that were sent to them. The second observation is that more than one stream of packets can be mixed together by one participant in such a way that the presence of any or all messages can be denied.
There have been only a handful of previous implementations of "chaffing and winnowing", most written in Perl [2,12]. These programs have just been proof-of-concept systems or have omitted such stages as a package-transform -- leaving them open to attack.
As already observed, in order to hide patterns in the plaintext that could help an attacker reconstruct the message by accumulating sections that fit, an "all-or-nothing transform" needs to be used. Rivest's original "chaffing and winnowing" paper suggested that his "Package Transform" [11] would be suitable.
This transform has some desirable properties. Although keys are used in the transform, it is not a cipher because the keys are not secret. Anyone with a copy of the transformed message can immediately convert it back into plaintext. However, it is infeasible to do this conversion or indeed to obtain any information at all about the original message, without having the entire transformed message available. This is exactly the property that "chaffing and winnowing" requires, since it means that an attacker has to guess exactly which sections of the data stream correspond to the message in order to get a decoding that generates anything other than random bits.
The message transform described by Rivest works as follows: consider m1, m2 ... ms to be the plaintext blocks, E an encryption function and K' a randomly chosen key. Then the encrypted blocks m'i are calculated to be:
m'i = mi xor E(K', i) for i = 1, ... ,s
The value of K' is transmitted to the receiver by sending the extra value M:
M = K' xor h1 xor h2 xor ... xor hs
where:
hi = E(K0, m'i xor i) for i = 1, ... , s
and K0 is a publicly known system wide key.
The receiver will have all of the m'i values along with M. They can retrieve K' by computing the values of hi and XORing them together. Once K' is known this can then be used to recover the values for mi.
The security of Rivest's "package transform" and other "all-or-nothing transforms" have been investigated by Anand Desai [7] and also commented upon by Mihir Bellare and Alexandra Boldyreva [5]. They concentrated on whether the transform is secure against exhaustive key search, and in particular in checking that such searches are slowed down by a factor that is equal to the number of blocks of ciphertext.
However, this is not quite the way in which the all-or-nothing transform is being used within a "chaffing and winnowing" system. In particular, Rivest's package transform does not create as much work as expected for an attacker who is trying a brute force attack to distinguish between message and chaff.
The problem is that the values for hi can be calculated once and then reused for any trial arrangement that incorporates the same section of the message in the same position. In particular, if the attacker has just tried the selection S1, S2, ... , Sn and now tries an alternative packet in position Si then all except one of the hi values can be reused in extracting the new trial value for K'.
What is necessary is for the value of hi to differ, depending upon the exact choice of message sections that has been made. A simple variation of the Rivest scheme that achieves this would be to calculate:
hi = E(K0, m'i xor Z) for i = 1, ... , s
where Z is the hash of the concatenated m' values:
Z = HASH(m'1, m'2, ... , m's)
HASH can be any cryptographically sound hash function, such as SHA-1 or MD5, or indeed a block cipher used as a hash function. One can further note that since the encryption function E is only used "one-way" it could be replaced by a hash -- meaning that only one type of cryptographic primitive is being used.
Using the value Z in this way pushes the cost of evaluating each trial arrangement up from as little as one encryption operation to at least s hash operations.
It will be further noted that the package transform described by Rivest uses a block cipher in counter mode that operates independently on each section mi of the message. In order to avoid problems with repetition of plaintext, the block number is XOR'd into the message value. In a "chaffing and winnowing" scheme these block numbers are all relatively small integers so that insufficient randomness may be injected to completely defeat an attacker who attempts to construct dictionaries of blocks at each position. Thus the security of this part of the transform is very heavily dependent upon selecting different random keys K'. Unless it is necessary to cater for parallel computation of this function, a defence-in-depth design philosophy makes it desirable to use a feedback mode for the encryption function.
The Regulation of Investigatory Powers Act 2000 [13] became part of UK law in July 2000. It covers a wide range of issues, from the rules for interception of communications through access to communications data (who talked to whom) to low-tech investigation techniques such as handling informers and following people down the street.
Part III of the Act relates to "encryption" and is currently (mid-2002) dormant, but is expected to become active later in the year. The basic idea of this part of the Act is that there is "protected information", which is either a message or some stored data. The authorities can, in suitable circumstances, serve a notice under s49 of the Act to require that the protected information be disclosed "in an intelligible form" (s50(1)(b)). It is an offence (s53), with up to two years gaol time to fail to comply. There are statutory defences (s53(2), s53(3), s53(4)) for such obvious issues as not having a suitable key to decrypt with, which means that you cannot be locked up for transporting random bits around.
If you are required to decrypt material then it is sufficient to deliver the plaintext. You may hand over your key if you prefer (s50(2)), but you are not in general obliged to do so. In some special circumstances the notice served under s49 can require the delivery of keys, but the Act specifically forbids access to "signature keys" in s49(9).
Chaffinch is a way of sending multiple messages within a single communication by means of a "chaffing and winnowing" style scheme. A "cover message" is always sent, which may be accompanied by further optional messages. The cover message is no shorter than the accompanying messages. In the face of legal challenge the cover message will always be the first to be revealed, and its contents should be chosen appropriately for this eventuality. It will be possible to "plausibly deny" that the optional messages exist, so they need not be revealed.
The system works by taking the cover message, splitting it into short sections and randomly interspersing "chaff" between these sections. The valid sections of the resulting communication are "signed" with a secret key so that the receiver can identify them, whereas the chaff is given a random "signing" value so that the receiver will ignore it. Anyone unaware of the secret key will face an impracticable amount of work in identifying precisely which sections form the message and thereby recovering the text.
The chaff can be composed either of completely random material, or it can be composed of further messages using different secret authentication keys. The treatment is the same as for the cover message; each further message is split into sections and then the appropriate secret key for that message authenticates each section by "signing" it. The resulting sections will act as chaff for the cover message and the cover message acts as chaff for them. Not all of the random chaff can be replaced by messages -- for otherwise revealing the next to last message would also reveal the last message. However, by careful design parameter choice, as discussed below, the Chaffinch system permits between one and fifteen further messages to be sent, depending upon their length.
Fig. 1 should make the general idea more clear. It shows a small part of a Chaffinch message, with the cover message (1) interleaved with two further messages (2) and (3). Note that the message sections are always in the correct order, but that a random choice is made as to the way in which the interleaving occurs, so in the example the first section of message 3 occurs before the first section of message 1.
Fig. 1. Conceptual view of a Chaffinch block
In Rivest's initial design he envisaged the use of a MAC to authenticate the message sections. He observed that by use of suitably long MAC values there would only be an infinitesimal chance of a random value attached to a piece of chaff being mistaken for a valid section of a message. He suggested a 64 bit MAC to ensure a false hit rate of less than one in 1019.
There is a problem with just using a MAC, pointed out by Bellare and Boldyreva [5]. If a message section recurs, then if the attached MAC values differ then this is an indication that one of the sections is message and the other is chaff. This can be used to reduce the time complexity of an attack.
However, the main difficulty with using large MACs is that they increase bandwidth usage, so within Chaffinch we use an alternative scheme. The secret authentication key is used to prime a stream cipher (we could have used a block cipher operating in output feedback mode). The resulting data is used, a few bits at a time, as a marker to show which message sections are part of the message. The other sections receive random values so that someone who knows the authentication key will know that they can be ignored. Since the authentication is independent of the message section values the Bellare-Boldyreva attack is not relevant.
To ensure that the authentication data will not be identical if the same key is used again with the same message, a random session value is incorporated into the cipher initialisation by hashing it with the authentication key. This session value is sent en claire to the receiver so that message reconstruction is possible. In order to avoid revealing how many messages are present within a single communication, the same session value is used for all of the messages being sent at the same time.
Although this authentication scheme uses less bandwidth (a few bits of cipher stream rather than 64 bits of MAC), it is now far more likely that a random value on a section of chaff will be mistaken for a valid authenticator. If only one message was being sent, it would be possible to choose another random value whenever a case of mistaken identity occurred. This would have to be done with care, so as to avoid any possibility that an attacker might detect non-random behaviour. However, we are trying to send multiple messages and if the next packet is from another message then you cannot change the authenticator on a single section. Clearly there are solutions to this, by choosing new session values and ordering the way in which misidentifications are checked for. However, this would be at the cost of some implementation complexity, with the consequent risk of errors that might allow an attacker to succeed in breaking the security of the system.
To keep the implementation simple, Chaffinch takes a completely different approach. No attempt is made to prevent random chaff from being recognised as a valid section of the message. Instead, the recipient does a "brute-force" search of the possible combinations of valid message sections, and the correct arrangement is detected when the decoding generates a message prepended by a valid hash of its contents. The details of this can be found in Sect. 4.2, but the executive summary is that by using 10 bits of the cipher stream as an authenticator, then on average it is necessary to consider 41 possible arrangements of message sections, and one time in ten thousand it will be necessary to consider 6,000 or more arrangements. This amount of effort is well within the capabilities of modern machines.
It is wise to have an agreement between sender and receiver as to what length messages may be, because this simplifies the brute force search algorithm and allows it to "prune" large numbers of cases, with consequent performance benefits. Therefore messages are padded to one of a small number of known lengths. By padding to the smallest of these known lengths we can ensure that apart from the presence of the cover message, it is not possible to determine how many further messages are present, even if some of them are revealed.
In order to deal with a cover message that is too long for the predefined lengths, we merely create a second Chaffinch block and append this to the first, with new random values and a new intermingling of message sections. The other messages are then distributed evenly across all available blocks. This algorithm, along with the insistence that the number of blocks is determined solely by the length of the cover message, prevents the leakage of information about the presence of any further messages.
We need to apply an "all-or-nothing" pre-processing function to the message text before it is split into sections and authenticated. This pre-processing prevents the attacker from picking out a message by using a probabilistic approach of guessing whether the next part of the data stream fits as the next message section, or whether it is just random chaff. Furthermore, the pseudo-random nature of the result of the pre-processing ensures that the message sections will be indistinguishable from the random chaff -- no statistical measurements will be able to tell them apart.
In Chaffinch we use an "all or nothing" scheme based on BEAR [1] rather than Rivest's package transform. Besides the weaknesses already discussed in Sect. 2.2, the package transform has the inconvenient property of adding an extra hash value to the length of each message -- leading to a number of implementation complexities. It also uses a session key and although this is transmitted in a visible manner (if one knows exactly where to look) a court of law might consider it be an encryption key and start treating Chaffinch as an encryption system rather than a way of transmitting authenticated messages. One of our design aims was to avoid systems that are prima facie encryption since pure authentication systems have special legal privileges. We believe that lay jury members will be especially impressed by the fact that we use BEAR in a keyless manner and the transformed message is sent in plain sight, albeit in a hard to locate fashion.
BEAR is usually described as a block cipher constructed from a keyed hash function and a stream cipher. These are combined in an unbalanced Feistel cipher structure where the left part (L) has the length of the output of the hash function and the right part (R) can be of arbitrary length.
Encryption is performed using a keyed hash function H(k) for some key k and a stream cipher S:
L = L xor H(k1, R)
R = R xor S(L)
L = L xor H(k2, R)
The decryption is done by exchanging k1 and k2. Any standard hash function, such as SHA-1 can be converted into a suitable keyed hash function by prepending the key to the input stream.
In Chaffinch, since we are not interested in secrecy but only in pre-processing into a sea of random bits, we don't use a key at all:
L = L xor H(R)
R = R xor S(L)
L = L xor H(R)
As we will see later in Sect. 4.2 the message text is preceded by some "red tape" which includes a randomly chosen nonce. This nonce contributes to the freshness whenever the same message is sent twice and also provides protection for messages with large amounts of padding -- which might otherwise be vulnerable to brute force attack. There is a small risk that a court might view this nonce as some sort of key. However, it changes with every message and is always revealed when the message is put into an intelligible form, so requests for it to be provided independently of the message text make no logical sense.
With the high-level design of Chaffinch described, we can now look at how this interacts with the UK's Regulation of Investigatory Powers Act.
If a s49 notice is served on a sender or a receiver, then they will be obliged to put their communications into an "intelligible form". A Chaffinch user could try and claim that their messages are not encrypted and hence are already intelligible, provided that one knows which sections to inspect. This might not impress a court, and previous papers already, in the limit, equate chaffing with encryption [9]. The court may also take the view that the use of keys to prime the stream cipher makes the system de facto encryption, even though the transforms made on the message itself are independent of these keys.
A Chaffinch user will, however, be able to respond to the s49 notice by providing the plaintext of the cover message. To prevent any dispute as to whether the plaintext is correct then the nonce for its session should also be provided. This will allow the authorities to recreate the message sections and see that they are present in the message. They will be able to do this without having access to the key that was used to create the authenticators and hence they will not have access to any other traffic, past or future.
If there are further hidden messages then the s49 notice will, presumably, have been written in such terms as to require that they are also revealed. However, if the sender and receiver are prepared to unlawfully conceal these messages, the authorities will find it impossible to demonstrate their presence. In the usual phrase, Chaffinch users have "plausible deniability".
If the authorities wish to go further they may use s51 to require keys to be divulged. However, the keys will have been used solely for generating "electronic signatures" to authenticate message sections and s49(9) prohibits any demand for this type of key. Whilst the RIP Act was being debated in the UK Parliament, there was some controversy surrounding this clause and the exact definition of an encryption key [3] and this might provide the basis of an argument that would convince the court.
If the legal argument fails and the Chaffinch keys must be revealed, then the same issues of "plausible deniability" arise as above. The user will need to divulge the key for cover messages (and any other messages they have revealed) because otherwise the authorities will know that they are being misled. However, undivulged messages whose keys stay secret will remain undetectable.
In this section we discuss some of the engineering decisions we took in implementing Chaffinch. To some extent, these choices are arbitrary, and other choices are valid, though they would not inter-operate with our code. However, there are some good reasons for picking values from particular ranges of possibilities and we explain the considerations that apply.
The first decision was the size of each message section. If it is large then more information can be sent but the larger it is, the greater the risk that some sort of bias might be detectable between n bytes of output of a random number generator and n bytes of output from the BEAR pre-processing. Naturally we would expect to use a good random number generator and BEAR primitives will give a reasonably random output, but keeping n small will frustrate this type of analysis. We settled on using 4 byte sections so that only major flaws in randomness would leak information.
Most email messages are short -- less than 4 kbytes long. We chose the maximum number of sections a message can use to be 1024 so that a typical email could be sent as a single Chaffinch packet. Each packet will, as we will see, occupy 10.5 kbytes on the wire. Of course, it is relatively easy to arrange for messages to be compressed before they are encoded. Since text will typically shrink to about 20% of its initial size this means that by adding an automatic compression stage to the Chaffinch system a single packet could transport a 20K message.
The sizes can now be chosen for the steganographically-concealed messages that can replace some of the chaff. These sizes need to be fixed in order to reduce the workload for the receiver who would otherwise have to try and detect messages at all possible sizes.
We need to provide at least 47 bytes of chaff to protect the confidentiality of the smallest message we send (and that message must be at least 47 sections long). This is because this gives a brute force attacker 94! / (47! X 47!) arrangements to consider (about 290) which is similar to the recommended complexity for long term security in Blaze et al [6]. In practice, we specified 64 sections of chaff and allowed messages to have sizes of 64, 128, 256, 512 or 1024 sections (256, 512, 1K, 2K or 4K bytes). This choice of sizes gives an attacker a minimum of 2116 arrangements to tackle, even if all other messages have been revealed except for a 64 section message and the accompanying chaff.
It will be recalled that chaff can be incorrectly identified as a section of the message if its randomly chosen authentication matches an expected value. However, there are only a small number of chaff sections between message sections; even the smallest message size of 64 is spread over just 2048 sections (one message section for every 31 of chaff). With an authenticator of 8 bits, there's only about a 12% chance of chaff being mistaken for part of the message. Of course, when the message is assembled and the BEAR pre-processing is undone, then the mistake will be detected. However, this will take effort, so reducing misidentification is desirable.
Misidentification is dominated by the presence of two n + 1 values between a section marked n and the section marked n+ 2. Clearly, other cases can occur (where an incorrect identification of n + 1 leads to the misidentification of which section is marked n + 2 etc) but sections that are marked correctly occur so much more often than by random chance that combinations of mistaken identity don't occur very often in practice.
So, as a first approximation, the number of combinations of sections that could form a message can be determined by a binomial distribution:
| n | |||
| ( | ) | px (1 - p)n - x | |
| x |
where n is the number of sections (64, 128, ..., 1024), x the number of misidentifications (and hence 2x the number of attempts necessary to decode the message) and p the probability of a misidentification. p is approximately (((2048 / (m-1)) - 2) / 2A where m is the number of sections and A the number of bits in the authentication data. Choosing A to be 10 leads to a manageable number of misidentifications: for 64 sections, 95% of the time one has a maximum of 128 attempts to decode the message.
It is possible to refine this model to consider other combinations of misidentification such as the sequence: n, n+1, n+2, n+1, n+2, n+3 ... which leads to three possible message constructions, but occurs more rarely. This combines with the mechanism already identified to give a further, 128 times less common, binomial distribution of 3, 6, 12, 24 ... possible arrangements.
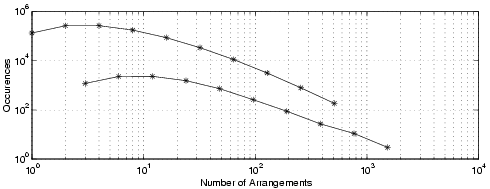
We verified this model by creating 1,000,000 Chaffinch messages with a 10 bit authenticator, 1024 message sections and plotted the resulting number of message arrangements in Fig. 2. The two overlapping binomial distributions can be clearly seen.

Fig. 2. Messages of 1024 sections, 1 million trials, log scales
When only 64 message sections were present, even more groups of binomial distributions occurred (because the extra chaff between message sections allowed more complicated interactions) as can be seen in Fig. 3.
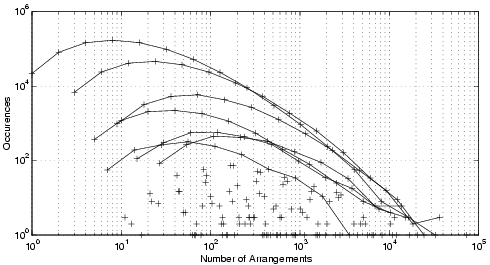
Fig. 3. Messages of 64 sections, 1 million trials, log scales
This analysis leads to a further refinement of the Chaffinch design. In order to ensure that a brute force attacker who is guessing keys will have the maximum amount of work to do, we process the authentication data with BEAR prior to splitting it up into 10-bit sections to mark the message. The attacker will therefore have to duplicate this processing before they can attempt to match their authentication stream with a message. If we did not do this then they would usually be able to conclude after a handful of matches that the authentication data was moving through the message sections too quickly to be valid.
Each message to be encoded by Chaffinch needs some further header data as shown in Fig. 4.
Fig. 4. Message format before BEAR preprocessing
nonce is the random value used to ensure that the pre-processing output is unique even where the same input message is present.
hash is a hash of all the other fields in this block and all preceding blocks, except the nonce values (which are ignored, to avoid any remaining possibility that they might be seen as a key).
count is a count of the message data bytes. One bit is also used to indicate that this is the last block in the whole Chaffinch communication.
session is a copy of the value described in Sect. 3.1 above (and shown in Fig. 1) that is used to provide uniqueness to the authentication scheme. It is reproduced here to prevent some types of message splicing attacks.
The message data is the text of the message to be sent and padding is any necessary zero valued bytes added to increase the total length of all the items shown to 256, 512, 1024, 2048 or 4096 bytes.
The hash only needs to be calculated over the current block in order to allow the receiver to identify when the correct set of sections has been accumulated. However, it is calculated over the entire message thus far in order to detect an attacker replacing, removing or substituting entire blocks.
The receiver needs to determine which sections form the message. This is relatively straightforward to do with a depth-first tree search with backtracking. The following pseudo-code shows the general technique:
sub decode()
for (n=0, i=0; ;i++) {
if (i < maxSections && expectSig[n] == actualSig[i]) {
// this section is signed correctly, so record it
blocks[n++] = i;
if (n == seekSections) {
// once have the required number of sections check
// if they form a valid part of the message
if (Validate(digest, last, blocks, chunks))
return TRUE;
// if not then look for alternative match
--n;
}
}
if (i >= limit[n]) {
// eventually no longer worthwhile looking for a match
if (n == 0)
return FALSE;
// so look for an alternative match
i = blocks[--n];
}
}
}
The limit array is filled in by searching backwards along the message to determine the last possible match for each signature. This then acts to prune the tree by indicating when it is not worthwhile searching for alternative matches because there is no possibility of filling in the rest of the blocks.
The Chaffinch system relies upon using different keys for different messages hidden in the same stream. In the original chaffing and winnowing paper, Rivest states that a standard key exchange protocol, such as Diffie-Hellman, could be used by the two communicating parties to exchange authentication keys. In the threat model that our system is addressing, this is somewhat more problematic.
Diffie-Hellman is pretty clearly an encryption system and is therefore subject to legal attack. If the authorities requested that a Diffie-Hellman exchange be put into an intelligible form then compliance would reveal whatever data had been transmitted over the link. However, if the Diffie-Hellman keys were discarded at the end of the conversation it would be possible to provide any plausible plaintext, rather than reveal some Chaffinch keying information. One might expect to be able to achieve this type of plausible deniability by using SSL to encrypt a Telnet session -- except that some SSL configurations use long term secrets. All in all, it might be wiser to arrange an out-of-band physical meeting in order to agree the shared secret authentication key.
It should be noted that Chaffinch requires a separate shared secret key for each message that is sent simultaneously, but the keys can be reused for subsequent messages. This leads to many interesting key sharing possibilities, including the idea of broadcast keys that allow for multi-way conversations. In particular keys can be agreed upon but never actually used. Chaffinch can be made more robust against coercion by agreeing extra keys per channel, one to be used to authenticate the traffic, and others to be revealed in extremis. If both parties to a conversation are being coerced at the same time then both revealing the same key may give plausibility to its veracity -- despite it never having been used, although considerable further difficulties may arise if someone misremembers the intended order of revelation.
A deniable encryption technique, such as the one presented by Beaver [4], could be used in order to exchange these two keys each time a message is sent. In order to make it even more plausible that the key revealed is actually the proper one it could also be used to authenticate some communications. This could be considered to be a special case of cover traffic within a Chaffinch channel.
There are some practical threats to the security of secret keys. It is important that they are never stored on disk, since various powers allow the authorities to inspect computer storage. Even if encryption hides the keys, the RIP Act permits the authorities to request that stored material is "put into an intelligible form".
As usual with key systems, it is possible to generate different keys for every message by means of a generating phrase that is hashed a different, reducing, number of times on each occasion. If the phrase is kept secret but a key is revealed then past traffic will be compromised (because the authorities can perform the hashes needed to construct keys used in the past) but future traffic will be protected. Alternatively, both forward and reverse secrecy can be achieved by creating new keys that are a result of encrypting a key with itself. This will provide backward secrecy.
It is a weakness of the Chaffinch system that the secrets that it uses are shared between sender and receiver. This means that either the sender or receiver of a message is in a position to reveal its contents and to compromise other messages sent with the same key. In an environment where both sender and receiver could be subject to simultaneous coercion to reveal these secrets it would be advisable to arrange for the secrets to be revealed in a pre-set order. This will minimise the rate of access to information achieved by the adversary for since half the effort spent on coercion will merely yield duplicate information -- and will also avoid a situation where the adversary knows that both parties are continuing to hide information. Once the adversary believes that all of the keys have been revealed then perhaps the coercion will cease.
When all messages within a single communication have been revealed then all that remains will be the random chaff. In some cases a Chaffinch user, particularly if subject to extreme forms of coercion, may wish to be able to demonstrate that no further messages remain hidden. This might be achieved by generating the chaff in a pseudo-random manner using a key for this purpose. Of course, once this key has been revealed then any communication containing N messages will be compromised as soon as N-1 message keys are known. In particular, if there is only a cover message then this will be immediately available. A better scheme would be to convert a suitable length array of zeros into a standard Chaffinch message, with nonce, hash, length, etc. This can then be used to provide the chaff sections, with the authentication values being truly random. Once all messages have been revealed, the remaining sections will compromise this message -- so there is no need to be able to regenerate the random data stream.
Other users will be satisfied with the security that is given by making the random chaff irreproducible. They will be unable to prove that no further messages remain to be discovered. Such users will know that no matter how extreme the coercion, and no matter how well or badly they face up to their situation, they will continue to tie up the resources of their adversaries in a fruitless task.
Finally, we note the possibility of providing further hidden channels within the chaff or within the (non-)authentication values that accompany the chaff. These channels could span many separate communications -- all that is needed is an agreement between sender and receiver as to where to look for them.
If a Chaffinch user comes under suspicion, their computer is likely to be seized and subjected to detailed forensic analysis. This may, of itself, yield copies of messages that have been communicated, either because they have been explicitly recorded or because details of the messages can be found in, or inferred from, system level files such as swap space. If more communications can be located than are accounted for by the information about messages or keys that have already been revealed, then the authorities will know that information is being withheld. Therefore Chaffinch can only be seen as one part of a communications security strategy in which systems such as steganographic filestores [8] may also play a part in providing system-wide plausible deniability.
We have shown how a practical confidential message passing system can be built that is based upon Rivest's "chaffing and winnowing" idea. By using an all-or-nothing system that utilises the variable block length cipher BEAR we have avoided the problems of pre-computation with Rivest's "package transform". The messages and also their authenticators are indistinguishable from random data, so further obfuscation can be achieved by disguising Chaffinch packets as other types of encryption.
As well as the cover message we have made it possible to send further confidential messages whose presence is plausibly deniable. We have proposed alternative schemes for handling the situation when the last message has been revealed, which allow a choice between escaping further coercion or tying up an attacker's resources indefinitely.
We have simplified message construction, and significantly reduced bandwidth requirements, by a probabilistic scheme that requires extra work by the receiver -- but a careful choice of design parameters keeps this work to a reasonable level. However, if the scheme was used for transmitting streaming media, then timing issues would require further study. We also assume that an attacker cannot observe the time taken to encode or decode any particular message.
We have analysed the ability of the system to withstand attack not just by attackers in the cryptographic realm but also by authorities with legal powers granted to them under the UK's Regulation of Investigatory Powers (RIP) Bill.
The system provides confidentiality, so even if communications are intercepted, it will not be possible to understand the content of the message. However, there is nothing in the Chaffinch design to hide the identities of sender and receiver; and in many cases security is compromised by the mere act of communication rather than by what it actually said. People looking for systems that are secure against this type of traffic analysis will need to look for other mechanisms beyond mere confidentiality and plausible deniability.
We would like to thank Dr Ross Anderson for his comments on drafts of this paper and for pointing out the simplification achieved by use of the BEAR cipher.