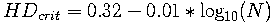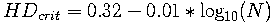Why False Match Probability does not Accumulate in Large Database Searches
Because the binomial tail of the
distribution
generated when different irises are compared attenuates so rapidly,
very small adjustments in the Decision Threshold allow truly huge
databases to be searched without suffering False Matches. The binomial
tail (solid curve) is governed by factorial terms since the comparisons
of bits in IrisCode phase sequences are Bernoulli trials; other biometrics
that are not based on complex random phase sequences do not have this
felicitous property. The rate of attenuation is such that each reduction
in the decision threshold by 1 percentage point in Hamming Distance (-0.01) causes
a nearly 10-fold further reduction in False Match probability. Some
illustrative values are given in this table of cumulatives under the tail
of the distribution:
| Decision Threshold |
Odds of False Match |
|
0.33 |
1 in 4 million |
|
0.32 |
1 in 26 million |
|
0.31 |
1 in 185 million |
|
0.30 |
1 in 1.5 billion |
|
0.29 |
1 in 13 billion |
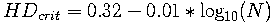
For all biometrics, the fact that the odds of making False Matches would
otherwise grow with
the number of enrolled templates in a database (rather like playing a game
of Russian Roulette an increasing number of times) means that if they can
operate in Identification mode at all, they
must reduce their decision thresholds relative to Verification mode.
A powerful aspect of the iris biometric based on
phase sequences, is that the binomial distributions generated by comparing
bits in IrisCodes have such rapidly attenuating tails that with minute
adjustments in decision threshold, national sized databases can be
accommodated while keeping the net False Match probability still minuscule.
For this reason, it is important to understand that the often cited figure
of "1 in a million" as the False Match rate for iris recognition
should be regarded as NET of the total database size. (A common error is
to multiply that rate by the database size to infer a net rate, ignoring
the intrinsic adjustment explained above.)
Further information about these issues can be found on the page:
statistical demands of identification vs verification.
Back to Main Page.