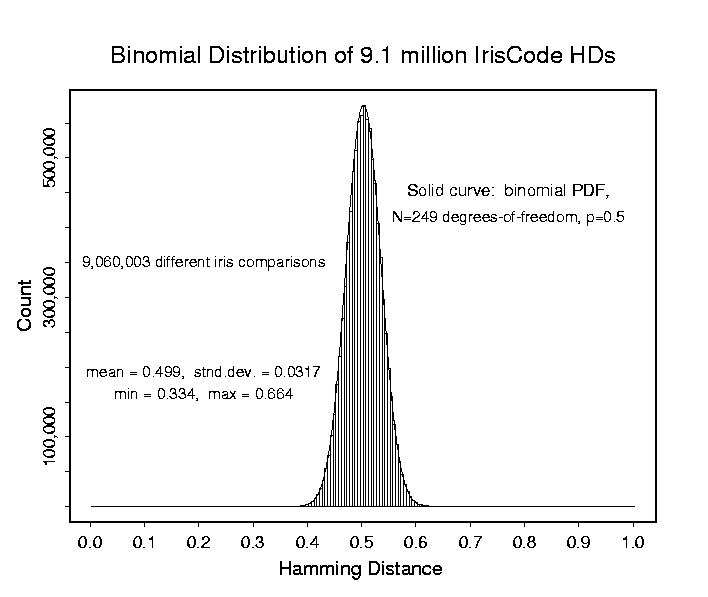
Histogram showing the outcomes of 9,060,003 comparisons between different pairs of irises. For each pair comparison, the percentage of their IrisCode bits that disagreed was computed and tallied as a fraction. Because of the zero-mean property of the wavelet demodulators, the computed coding bits are equally likely to be 1 or 0. Thus when any corresponding bits of two different IrisCodes are compared, each of the four combinations (00), (01), (10), (11) has equal probability. In two of these cases the bits agree, and in the other two they disagree. Therefore one would expect on average 50% of the bits between two different IrisCodes to agree by chance. The above histogram presenting comparisons between 9.1 million different pairings of irises shows a mean fraction of 0.499 of their IrisCode bits agreeing by chance.
The standard deviation of this distribution, 0.0317, reveals the effective number of independent bits (binary degrees of freedom) when IrisCodes are compared. Because of correlations within irises and within computed IrisCodes, the number of degrees of freedom is considerably smaller than the number of bits computed. But even correlated Bernoulli trials (coin tosses) generate binomial distributions; the effect of their correlations is equivalent to reducing the effective number of Bernoulli trials. For comparisons between different pairs of IrisCodes, the distribution shown above corresponds to that for the fraction of "heads" that one would get in runs of 249 tosses of a fair coin. This is a binomial distribution, with parameters p=q=0.5 and N=249 Bernoulli trials (coin tosses). The solid curve in the above histogram is a plot of such a binomial probability distribution. It gives an extremely exact fit to the observed distribution, as may be seen by comparing the solid curve to the data histogram.
The conclusion is that Hamming Distance comparisons between different IrisCodes are binomially distributed, with 249 degrees of freedom. The important corollary of this conclusion is that the tails of such distributions are dominated by factorial combinatorial factors, which attenuate at astronomic rates. This property makes it extremely improbable that two different IrisCodes might happen to agree just by chance in, say, more than 2/3rds of their bits (making a Hamming Distance below 0.33 in the above plot). The confidence levels against such an occurence are the reason why iris recognition can afford to search extremely large databases, even on a national scale, with negligible probability of making even a single false match.
A reprint of the full scientific paper published in Pattern Recognition analyzing the results of 9.1 million IrisCode comparisons is available here.