Here is a schedule of work for supervisions with Graham Titmus.
Your solutions should be handed in to the main Porters' Lodge at Caius College by noon on the day preceding the supervision. The supervisions will be held in my room at Caius, P11 Tree Court, as follows:
| Tuesday | 14:00 | |
| 15:00 | ||
| 16:00 | ||
| 17:00 | ||
| Wednesday | 14:00 |
A number q is rational if q = a/b, where a and b are integers with b not 0. Construct a program to perform the usual arithmetic operation on rational numbers: addition, subtraction, multiplication, division and equality. The program should also contain a function to convert a rational number to a suitable text representation.
Tackle this by doing the following
Hint: you might need to implement Euclid's algorithm for the greatest common divisor to use in the above.
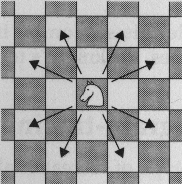
In addition consider the following problem, known as the Knight's tour.
Can a knight moves to all the places on a chess board but only landing on each one once?
Each time the knight has a choice of moves:-

To start work on this problem do the following work only.
fun prefix [ ] [ ] = [ ]
| prefix (x::xs) (y::ys) = (x::y)::prefix xs ys;
fun sep [ ] = [[ ],[ ]]
| sep [x] = [[x],[ ]]
| sep (x::y::rest) = prefix [x,y] (sep rest);
fun merge [[ ],y] = y : int list
| merge [x,[ ]] = x
| merge [x::xs, y::ys] =
if x < y then x :: merge [xs, y::ys]
else y :: merge [x::xs, ys];
Next do exercises from chaper 6 up to and including chapter 9.
Finally, consider the problem of getting out of a maze. Below is a schematic of the maze at Hampton Court.
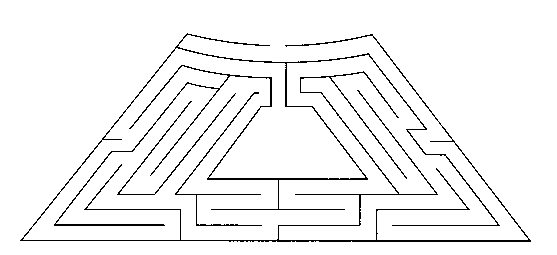
Code and test the maze program that we considered last week. Document your design, your code and your test data.
Write a shortest path finding program to find the distance from the front (1) to the back (18) of the Guildhall. As before you should split this into three parts, design, code and test making each stage visible. Identify how you needed to extedn the maze program to solve this problem.
You can either start from the map of Cambridge and measure the points yourself or use this list:-
val roads = [(1,2,0.4, 1),(2,1,1.5,1),(2,3,1.0,1),
(3,4,1.1,1),(4,5,0.8,1),(4,7,1.4,1),
(5,6,1.0,1),(6,7,2.6,1),(7,1,1.7,1),
(8,9,16.5,2),(10,9,2.0,2),
(10,11,2.4,2),(9,12,0.3,2),(12,13,2.5,2),
(12,19,4.7,2),(12,14,2.0,1),(18,14,5.8,2),
(19,18,1.0,2),(18,17,2.8,2),(14,15,0.5,1),
(15,16,1.5,1),(15,18,2.1,1),(18,10,1.8,1),
(17,22,3.0,2),(22,16,2.0,2),(22,20,2.7,2),
(17,19,4.4,2),(19,20,3.0,2),(20,21,1.5,2),
(17,19,4.4,2),(19,20,3.0,2),(20,21,1.5,2),
(21,16,2.3,2),(21,23,3.7,2),(23,26,7.5,2),
(23,25,3.2,2),(5,25,2.1,2),(24,25,1.2,1),
(26,8,8.3,2),(16,27,2.0,2),(27,24,2.4,2),
(27,3,1.8,1)]
where each entry is as follows
(node1, node2, distance, 1=one way|2=bidirectional)
Aim to clearly document how your code works.
Then try to add a new link (8,6,3.5,2) from the matrix of
connections and see what difference it makes to the distance.
Make the maze and City streets problem into Lazy List versions.
I want a description of how you designed your solution. Don't look for short-cuts, do a strightforward exhaustive search and return the first solution. Try it out on smaller custom boards for which a solution does exist and make sure it finds them.
datatype A = Z
| Cell of int ref * A ref * A ref;
Each cell contains an integer value and pointers to the cells immediately
to its right and above itself. These three components are all mutable
so that the arrangement of the cells and the integers they contain can
change during use. The constructor Z can be used in an A ref to allow
a cluster to have a boundary rather than continuing through unbounded
chains of cells.
Define a function mkrow(n) of type int->A that will return a row of length n + 1 cells initialised with zeros. For instance:
mkrow(1) = Cell(ref 0, ref(Cell(ref 0, ref Z, ref Z)), ref Z)
Define a function zip (rowl, row2) of type A*A->A that will return row1 with row2 joined above it. This function is entitled to change some of the ref A pointers in rowl. For example
val root = zip(mkrow(3), mkrow(2));would give root a value representing the following arrangement.
0 ----> 0 ----> 0
^ ^ ^
| | |
| | |
root : 0 ----> 0 ----> 0 ---> 0
Next define a function mkarr (m, n) of type (int* int) ->A that will return a value representing a rectangular array of n + 1 rows each ofwhich are of length m + 1 in which each cell is initialised to zero.
Paths originating from the bottom leftmost cell (which will be referred to by the variable root) are represented by values of the type dir list where dir is declared as follows:
datatype dir = Right | Up;Finally define a function inc-path-cells of type A-> dir list -> unit that will increment the integers in all the cells that lie on a specified path within a given collection of cells. For instance after root had been set up as above, the two calls
inc-path-cells root [Right, Up, Right]; inc-path-cells root [Right, Right, Right];would leave root representing the following arrangement:
0 ----> 1 ----> 1
^ ^ ^
| | |
| | |
root : 2 ----> 2 ----> 1 ---> 1
You may assume that the path does not try to reach cells outside the
given arrangement.
Consider whether Computer Scientists are Professionals. Look at the code of conduct of one of the professional bodies (ACM or BCS) and comment on its policies in the light of your discussion of the first question.
You may find the following site useful - Ethics and Intellectual Property Resources on the Web.