Michaelmas Term 1997

Week 1 (due w/b 13-10-97)

Week 2 (due w/b 20-10-97)

Find reference on WWW to the algorithm for calculating leap years. Write an implementation of that as a predicate isleap which will work for well into the next millenium. Use that to write Qu12 from last week in ML.

Week 3 (due w/b 27-Oct-97)

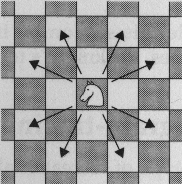
Can a knight moves to all the places on a chess board but only landing on each one once?

Each time the knight has a choice of moves:-

To start work on this problem do the following work only.

1. Decide upon a representation for the chessboard and write a function to generate a board with no moves yet taken place on it. Name the function makeboard which is of type
   int -> board_type
   where board_type is up to you. The int part is the size of the board which is square.
2. Write a function which when given a poistion of a knight and a board will return a list of the possible moves. The functions shoudl be called generateMoves and will be of type
   (int * int) * board_type -> (int * int) list
   where int * int is a coordinate on the board. [] being returned when no moves exist.
3. Test these functions by placing the knight in various positions and checking that you get back the correct result. State the criteria you use to choose test values.

Week 4 (due w/b 3-11-97)

fun prefix [ ]  [ ] = [ ]
  | prefix (x::xs) (y::ys) = (x::y)::prefix xs ys;

fun sep [ ] = [[ ],[ ]]
  | sep [x] = [[x],[ ]]
  | sep (x::y::rest) = prefix [x,y]  (sep rest);

fun merge [[ ],y] = y : int list
  | merge [x,[ ]] = x
  | merge [x::xs, y::ys] =
           if x < y then x :: merge [xs, y::ys]
                  else y :: merge [x::xs, ys];

1. Deduce the ML type of the function prefix showing your method of deduction in detail. Verify by evaluating the result of the call prefix [1,2,3] [[4],[5],[6]];
2. Give a correctly-typed call to prefix that will generate an exception when evaluated. Explain why this is possible despite the type checking by the compiler.
3. What values do sep[l,2,3,4,5,6,7,8] and sep[1,2,3,4,5,6,7] yield?
4. Deduce the ML type of merge, showing your working in detail, and explain why the omision of `: int list' would lead to an error.
5. Give an ML definition of the standard library function map.

1. What sort of data structure could you use to represent this?
2. Label up the maze as necessary and construct your representation.
3. Design (but you do not have to code) your algorithm for escaping from the maze.

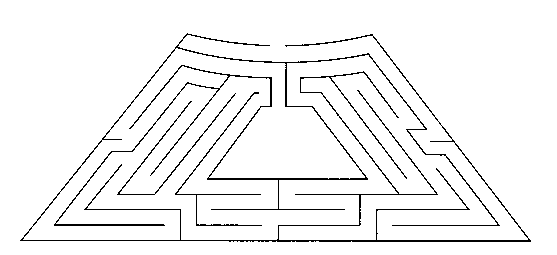
   A copy of the code for walking the maze shown above can be found here.

Week 5 (due w/b 10-11-97)

Write a shortest path finding program to find the distance from the front (1) to the back (18) of the Guildhall.

You can either start from the map of Cambridge and measure the points yourself or use this list:-

val roads = [(1,2,0.4, 1),(2,1,1.5,1),(2,3,1.0,1),
             (3,4,1.1,1),(4,5,0.8,1),(4,7,1.4,1),
             (5,6,1.0,1),(6,7,2.6,1),(7,1,1.7,1),
             (6,8,3.5,2),(8,9,16.5,2),(10,9,2.0,2),
             (10,11,2.4,2),(9,12,0.3,2),(12,13,2.5,2),
             (12,19,4.7,2),(12,14,2.0,1),(18,14,5.8,2),
             (19,18,1.0,2),(18,17,2.8,2),(14,15,0.5,1),
             (15,16,1.5,1),(15,18,2.1,1),(18,10,1.8,1),
             (17,22,3.0,2),(22,16,2.0,2),(22,20,2.7,2),
             (17,19,4.4,2),(19,20,3.0,2),(20,21,1.5,2),
             (21,16,2.3,2),(21,23,3.7,2),(23,26,7.5,2),
             (23,25,3.2,2),(5,25,2.1,2),(24,25,1.2,1),
             (26,8,8.3,2),(16,27,2.0,2),(27,24,2.4,2),
             (27,3,1.8,1)]

    (node1, node2, distance, 1=one way|2=bidirectional)

Try to finish the Knight's tour problem and find a solution. You should use a list of (x,y) 2-tuples to represent the board and show that the solution is a magic square. You need to think about how to handle the backtracking and avoid going down the same solution path twice. You could test your algorithm on a smaller board if you like.

I want a description of how you designed your solution. Don't look for short-cuts, do a strightforward exhaustive search and return the first solution. Click here to see a answer.

Week 6 (due w/b 17-11-97)

Use a lazy list datatype to implement a random number generator. It should return a random (real) number between 0 and 1 and a function to call to get the next. You should find a suitable algorithm from a textbook for this, up to 4 significant figures will be more than adequate.

Get the route finding and knight's tour programs to work.

Week 7 (due w/b 24-11-97)

1. InsertItem: (('a * 'a) -> boolean) * 'a * 'a tree) -> 'a tree
   given an item returns a new tree with the item inserted. Make sure your function obeys the type rule! What is the ('a * 'a) -> boolean for?
2. BuildTree: ('a list, ('a * 'a) -> boolean)) -> 'a tree
   given alist of items returns a tree with the items in order.
3. BuildBalancedTree: ('a list, ('a * 'a) -> boolean)) -> 'a tree
   given alist of items returns a tree with the items in order and also the tree is a balanced as possible. To do this you need to think about how you can rewrite a tree to preserve order but have a different arrangment of branches.
4. You could consider building curried versions of these functions as and examine the types you get back when you hand them a comparison function.
5. Fringe: ('a tree) -> 'a list
   given a tree returns the items in order.
6. TreesEqual ('a tree * 'a tree) -> boolean
   given two trees returns whether they are equal or not. You can do this by calling Fringe on each list and then comparing the two lists. However, try to do it by only examining as much of the tree as is necessary by creating a lazy fringe function

A solution to building balanced trees is given here.

Week 8 (due w/b 1-12-97)

1994 paper 1 question 6. The following ML declaration introduces a data type that can be used to represent a potentially infinite arrangement of cells at positions with integer coordinates in the first quadrant of the x - y plane:

datatype A = Z 
           | Cell of int ref * A ref * A ref;

Define a function mkrow(n) of type int->A that will return a row of length n + 1 cells initialised with zeros. For instance:

mkrow(1) = Cell(ref 0, ref(Cell(ref 0, ref Z, ref Z)), ref Z)

Define a function zip (rowl, row2) of type A*A->A that will return row1 with row2 joined above it. This function is entitled to change some of the ref A pointers in rowl. For example

val root = zip(mkrow(3), mkrow(2));

                     0 ----> 0 ----> 0
                     ^       ^       ^
                     |       |       |
                     |       |       |
              root : 0 ----> 0 ----> 0 ---> 0

Next define a function mkarr (m, n) of type (int* int) ->A that will return a value representing a rectangular array of n + 1 rows each of which are of length m + 1 in which each cell is initialised to zero.

Paths originating from the bottom leftmost cell (which will be referred to by the variable root) are represented by values of the type dir list where dir is declared as follows:

datatype dir = Right | Up;

inc-path-cells root [Right, Up, Right];
inc-path-cells root [Right, Right, Right];

                     0 ----> 1 ----> 1
                     ^       ^       ^
                     |       |       |
                     |       |       |
              root : 2 ----> 2 ----> 1 ---> 1

Lent Term 1998

Week 1 (due w/b 19-1-98)

Look at the following site Ethics and Intellectual Property Resources on the Web.

Find the paper "Why Software Should Be Free" and critically evaluate Richard Stallman's position.

Week 2 (due w/b 26-1-98)

Consider the limitation on the use of strong encryption proposed for the USA in relation to privacy. You may like to look at some information on the Privacy homepage.

Week 3 (due w/b 2-2-98)

Week 4 (due w/b 9-2-98)

Week 5 (due w/b 16-2-98)

A date is made up of three integer values, for day, month and year. (Make sure you are Y2K compliant!) Write three procedures.

• Feb29th which should take a date and return true iff the date (eg 29/2/96) is legal. ie this is the leap year predicate.
• Weekday should return true if the date falls on one of the days other than Saturday or Sunday.
• next when given a date returns tomorrows date.

You should explain how your functins work and have tested them using some suitable test data. Your not need to worry about dates in other than the current calendar system.

Week 6 (due w/b 23-2-98)

You should have several types of event. A simple single event which happens on one date, and repeated events, which have a start and stop date and happen at each intervening specified day (such as every week on tursday).

Write code to create a sorted event list. (If you know about interfaces then write an interface and an implementation to it.)

Think about how you might handle the two event types if the final application of this work were a diary system.

Week 7 (due w/b 2-3-98)

• Get the diary working using doubly linked list with single events and some attempt at regular repeated events such as daily or weekly.
• Use the standard Date class and extend it to add any methods you need.
• Add a facility to save a diary to a file and reload it.

Also write a answer to the following exam style question:-

What is the meaning of the words static, public and private in relation to variables and methods in a class definition. Illustrate your answer with code fragments.

Why is the ability to declare pointers in java not a serious handicap to the use of the language?

Week 8 (due w/b 9-3-98)

A graphics class G contains a method public void drawLatA(float angle, int length).

Write two versions of the rose-drawing class. One using recursion and the other iteration. The argument to the class constructor should be the length of the North line in integer units.

Try to write these as if in an exam, then have a go at writing an Applet to display it.

Easter Term Supervisions

Week 1 (due w/b 27-4-97)

Write a Z schema to define a legal DATE in the Gregorian calendar. Try to get it to exclude leap days. What is the relationship between a formal method like Z and code?

What are the advantages and disadvantages of using formal methods?

Week 2 (due w/b 4-5-97)

1. Describe the facilities in Java for modelling data by means of arrays and objects. [12 marks]

   Illustrate your answer by specifying some data types to model a map. This should include points (specifying latitude and longitude), junctions (specifying a point and the roads incident at the junction) and road segments (specifying the junxctions at each end, a name and some intermediate points between the ends). [8 marks]

2. Paper 1 Question 5 from 1997

Week 3 (due w/b 11-5-97)

 

University of Cambridge
Computer Laboratory
New Museums Site
Pembroke Street
Cambridge   CB2 3QG
England

E-mail: Graham.Titmus@cl.cam.ac.uk
Telephone: +44 1223 334620
Facsimile: +44 1223 334678