To find the previous work set this term go to previous
weeks, for previous term go to Michaelmas or
Lent
All work should be handed in by midday of the day before the supervision
(except for Monday supervisions when it should be in by Friday lunchtime
or send by email).
Current work
This week we will go over the ML and Modula-3 examination questions
from some previous examination papers. Make sure you have read through
your ML and Modula-3 lecture notes.
Week 1 (due w/b 28-4-97)
This week we will go over the ML and Modula-3 examination questions
from some previous examination papers. Make sure you have read through
your ML and Modula-3 lecture notes.
Week 2 (due w/b 5-5-97)
Operating systems and PP&E
Week 3 (due w/b 12-5-97)
Operating systems supervision
Week 4 (due w/b 19-5-97)
Attempt the two question 1995 paper 11 question 7 and 1996 papaer 10 question 7.
Week 1 (due w/b 20-1-97)
How can cyberspace be controlled by regulation or legislation to
make it civilised?
Week 2 (due w/b 27-1-97)
Look at the following site
Ethics
and Intellectual Property Resources on the Web.
Find the paper "Why Software Should Be Free" and critically evaluate
Richard Stallman's position.
Week 3 (due w/b 3-2-97)
Do questions 2, 5 and 6 from Paper 1 in 1976.
Week 4 (due w/b 10-2-97)
No work will be set this week and no supervisions held.
Week 5 (due w/b 17-2-97)
Modula-3 supervisions start this week.
Try to generate a syntax chart that is capable of describing any ammount
of money (UK currency) that could be given in change as a text string, e.g.
Five pounds 27p.
Then write, compile and test a function to computer factorials. Can you
get it to break? Write the code in ML and think about how you did things
differently and why.
Week 6 (due w/b 24-2-97)
Write a function to print out a text representation of an ammount of change
using the syntax diagrem you wrote last week.
Also write a function to compute which coins to use to give that ammount of
change. You should ensure that you hold the available coints in a suitable
data structure that is updated as coins are used and is persistant across
runs of the program.
Consider but do not code for error conditions that could arrise.
Week 7 (due w/b 3-3-97)
Collect the code to convert a sum of money into a text string into a module
which implements the interface
INTERFACE PrintMoney;
IMPORT Text;
PROCEDURE MoneyToText (pounds, pence: CARDINAL): TEXT;
END PrintMoney.
Also write a new module which uses objects to implement a till. Each till
should be capable of holding the money it contains and implement the following
methods as in the interface.
INTERFACE Till;
TYPE T<: Public;
Public = OBJECT
METHODS
init(number: CARDINAL) : T;
close(): NULL;
giveChange(pounds,pence: CARDINAL): TEXT
END;
END Till.
where the storage of coins in the object is implemented as follows
Public = OBJECT
coins: ARRAY CoinType OF CARDINAL;
METHODS
....
END;
Note that you will probably need CoinType in both modules so put it in another
one
TYPE CoinType = {L20,L10,L5,L1,p50,p20,p10,p5,p2p1};
Construct a suitable test harness for this and try to swap your implementations
with someone else to test for portability.
Week 8 (due w/b 10-3-97)
Do questions 9 and 10 from paper 1 of the 1996 examination. Spend 1 hour
in total onn the two and then go and try to code up your answers to test
how well you did.
Week 1 (due w/b 14-10-96)
Questions 1-12 from Goldschlager & Lister Chapter 2.
Week 2 (due w/b 21-10-96)
Questions 4.1 and 4.2 from Lecture notes.
Find reference on WWW to the algorithm for calculating leap years.
Write an implementation of that as a predicate isleap which will work for
well into the next millenium. Use that to write Qu12 from last week in ML.
Week 3 (due w/b 28-Oct-96)
Do exercices 5.1 to 5.7 but not 5.4.
In addition consider the following problem, known as the Knight's tour.
Can a knight moves to all the places on a chess board but only landing on
each one once?
Each time the knight has a choice of moves:-
To start work on this problem do the following work only.
- Decide upon a representation for the chessboard and write a function
to generate a board with no moves yet taken place on it. Name the function
makeboard which is of type
int -> board_type
where
board_type is up to you. The int part is the size of the board
which is square.
- Write a function which when given a poistion of a knight and a board
will return a list of the possible moves. The functions shoudl be called
generateMoves and will be of type
(int * int) * board_type ->
(int * int) list
where int * int is a coordinate on the board.
[] being returned when no moves exist.
- Test these functions by placing the knight in various positions and
checking that you get back the correct result. State the criteria you
use to choose test values.
Week 4 (due w/b 4-11-96)
Study the following ML function definitions and answer the questions below:
fun prefix [ ] [ ] = [ ]
| prefix (x::xs) (y::ys) = (x::y)::prefix xs ys;
fun sep [ ] = [[ ],[ ]]
| sep [x] = [[x],[ ]]
| sep (x::y::rest) = prefix [x,y] (sep rest);
fun merge [[ ],y] = y : int list
| merge [x,[ ]] =x
| merge [x::xs, y::ys] =
if x < y then x :: merge [xs, y::ys]
else y :: merge [x::xs, ys];
-
Deduce the ML type of the function prefix showing your method of deduction
in detail. Verify by evaluating the result of the call
prefix [1,2,3] [[4],[5],[6]];
-
Give a correctly-typed call to prefix that will generate an exception when
evaluated. Explain why this is possible despite the type checking by the
compiler.
-
What values do sep[l,2,3,4,5,6,7,8] and
sep[1,2,3,4,5,6,7] yield?
-
Deduce the ML type of merge, showing your working in detail, and explain
why the ornision of `: int list'
would lead to an error.
-
Give an ML definition of the standard library function map.
Finally, consider the problem of getting out of a maze. Below is a
schematic of the maze at Hampton Court.
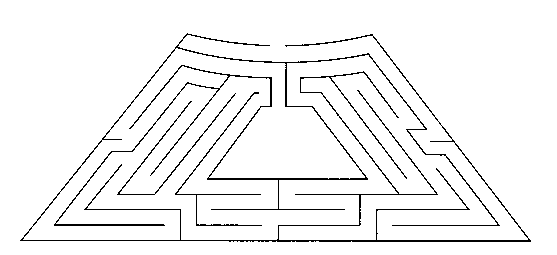
- What sort of data structure could you use to represent this?
- Label up the maze as necessary and construct your representation.
- Design (but you do not have to code) your algorithm for escaping
from the maze.
Week 5 (due w/b 11-10-96)
Try to finish the Knight's tour problem and find a solution. You should use
a list of (x,y) 2-tuples to represent the board and show that the solution is a
magic square. You need to think about how to handle the backtracking and avoid
going down the same solution path twice. You could test your algorithm on a
smaller board if you like.
I want a description of how you designed your solution. Don't look for short-cuts,
do a strightforward exhaustive search and return the first solution. Click
here to see a answer.
If you don't run out of time on that then you can implement the Maze walking
program as tree traversal. You have noticed that there are loops - how are you
going to prevent youself going around in circles.
Hint: Note that the quickest route
out is found by breadth-first search of the network. This can't be done just using
the stack - look in ML for the working programmer to see how to do breadth first
search on a tree and implement that for your network. Represent the network as
a list of connections [(a,b), (c,d)].
A copy of the code for walking the maze shown above can be found
here.
Week 6 (due w/b 18-11-96)
Binary (or higher) trees are a common data structure. Using the datatype:-
datatype 'a tree = leaf | node of 'a tree * 'a * 'a tree;
Construct the following functions
- InsertItem: (('a * 'a) -> boolean) * 'a * 'a tree) -> 'a tree
given an item returns a new tree with the item inserted. Make sure
your function obeys the type rule! What is the ('a * 'a) -> boolean
for?
- BuildTree: ('a list, ('a * 'a) -> boolean)) -> 'a tree
given alist of items returns a tree with the items in order.
- BuildBalancedTree: ('a list, ('a * 'a) -> boolean)) -> 'a tree
given alist of items returns a tree with the items in order and also
the tree is a balanced as possible. To do this you need to think about
how you can rewrite a tree to preserve order but have a different
arrangment of branches.
- You could consider building curried versions of these functions as and
examine the types you get back when you hand them a comparison function.
- Fringe: ('a tree) -> 'a list
given a tree returns the items in order.
- TreesEqual ('a tree * 'a tree) -> boolean
given two trees returns whether they are equal or not. You can do this by
calling Fringe on each list and then comparing the two lists. However,
try to do it by only examining as much of the tree as is necessary.
Remember to describe your algorithm as well as coding it. Include printout
to demonstrate that your code functions correctly and parts 3 and 5 discuss
how you chose your test data.
Week 7 (due w/b 25-11-96)
Use a lazy list datatype to implement a random number generator. It should
return a random (real) number between 0 and 1 and a function to call to get
the next. You should find a suitable algorithm from a textbook for this,
up to 4 significant figures will be more than adequate.
Then use this to insert the items in a balanced tree - building it balanced as
you go.
A solution to this is given
here.
Also implement the maze walking algorithm as a stream, this should allow you
to get back the best route, then the next best route etc until you have no more
non-circular routes. You can use the maze from earlier weeks and the queue
based traversal method for this.
A solution to this which should be loaded after the week 6 maze walking
code is given here.
Week 8 (due w/b 2-11-96)
University of Cambridge
Computer Laboratory
New Museums Site
Pembroke Street
Cambridge CB2 3QG
England
E-mail: Graham.Titmus@cl.cam.ac.uk
Telephone: +44 1223 334620
Facsimile: +44 1223 334678


