Getting started with PyTorch

This is a brief introduction to PyTorch, designed to complement the IB Data Science course. It assumes you’re familiar with the idea of maximum likelihood estimation. We’ll use PyTorch to represent a probability model for regression, and fit it.

There are many other tutorials on PyTorch, including the tutorial in the official documentation. They typically present PyTorch as a software library, and go into much more depth on tensors and GPUs and so on. But they often don’t give much guidance on how to use PyTorch for data science.

In this tutorial we’ll work with the data behind the xkcd 2048 comic on curve-fitting. First, load the dataset:

url = 'https://www.cl.cam.ac.uk/teaching/current/DataSci/data/xkcd.csv'
xkcd = pandas.read_csv(url)

fig,ax = plt.subplots(figsize=(4,3))
ax.scatter(xkcd.x, xkcd.y)
plt.show()

Step 1. Fitting with scipy

Consider the probability model \[ Y_i \sim a + b x_i + c x_i^2 + N(0,\sigma^2). \] We can fit this model to the dataset using maximum likelihood estimation. The fitted function \(\hat{a}+\hat{b}x+\hat{c}x^2\) is shown below. The fitted standard deviation \(\hat{\sigma}\) is also shown, by a ribbon extending above and below the fitted line by \(2\hat{\sigma}\).

def μ(x, a,b,c): return a + b*x + c*x**2

def μ(x, a,b,c):
    return a + b*x + c*x**2

def logPr(y, x,a,b,c,σ):
    return np.sum(scipy.stats.norm.logpdf(y, loc=μ(x,a,b,c), scale=np.sqrt(σ**2)))

ahat,bhat,chat,σhat = scipy.optimize.fmin(lambda θ: -logPr(xkcd.y, xkcd.x, *θ), [1,1,0,1])
# Expected answer for log likelihood: -61.575367

fig,ax = plt.subplots(figsize=(4,3))
ax.scatter(xkcd.x, xkcd.y)
xnew = np.linspace(0,10,100)
ynew = μ(xnew, ahat, bhat, chat)
ax.plot(xnew, ynew, color='black')
ax.fill_between(xnew, ynew-2*σhat, ynew+2*σhat, color='steelblue', alpha=.6)
plt.show()

Step 2. Defining functions in PyTorch

To fit our probability model, we have to maximize the log likelihood function, \[ \log\operatorname{Pr}(y;x,a,b,c,\sigma). \] Here, \(x\) and \(y\) are the data that we’re given (both of them numpy vectors of 31 elements), and the other four parameters are unknowns that we want to maximize over.

In PyTorch, we define a function with unknown parameters by creating a class that inherits from torch.nn.Module. Declare any unknowns in the constructor, wrapping them in torch.nn.Parameter to tell PyTorch that they are to be optimized over. Also, define a forward method that does the work of actually computing the value of the function; this will be invoked automatically when we call our function object. Here’s an example:

import torch
import torch.nn

class MyFunction(nn.Module):
    def __init__(self):
        super().__init__()
        self.θ = nn.Parameter(torch.tensor(1.0))
    def forward(self, x):
        return (x - self.θ) ** 2

f = MyFunction()
f(torch.tensor(3.1))

Anything numerical we do in PyTorch, we do on torch.tensor objects. These are similar to numpy arrays; there are tensor methods that mimic many of the numpy array methods; and simple Python arithmetical operations like - and ** are overridden to work on tensors. When we implement a function using only tensor operations, then PyTorch can automatically compute the derivative of our function, and this is what allows it to do efficient optimization using gradient descent.

x = torch.tensor(xkcd.x, dtype=torch.float)
y = torch.tensor(xkcd.y, dtype=torch.float)

import torch
import torch.nn as nn

class LogPr(nn.Module):
    def __init__(self):
        super().__init__()
        self.a = nn.Parameter(torch.tensor(1.0))
        self.b = nn.Parameter(torch.tensor(1.0))
        self.c = nn.Parameter(torch.tensor(0.0))
        self.σ = nn.Parameter(torch.tensor(1.0))
    def μ(self, x):
        return self.a + self.b * x + self.c * x**2
    def forward(self, y, x):
        σ2 = self.σ ** 2
        return torch.sum(- 0.5*torch.log(2*np.pi*σ2) - torch.pow(y - self.μ(x), 2) / (2*σ2))
    
x = torch.tensor(xkcd.x, dtype=torch.float)
y = torch.tensor(xkcd.y, dtype=torch.float)
logPr = LogPr()
logPr(y, x)
# expected output: tensor(-185.3153, grad_fn=<SumBackward0>)

Step 3. Optimization in PyTorch

PyTorch is, at its core, a library to make it easy to minimize complicated functions using gradient descent.

• We define a function (involving parameters to be optimized over),
• we create an optimizer object that knows about these parameters,
• then we repeatedly compute gradients with respect to these parameters and take a step in the direction of steepest descent. (There are several different optimizers that use different strategies for choosing step size; the Adam optimizer, used in the code below, is good for neural networks, and a bit crummy for simple optimizations like this one!)

import torch

f = MyFunction()
optimizer = torch.optim.Adam(f.parameters())

for epoch in range(5000):  # number of gradient-descent steps
    optimizer.zero_grad()
    val = f(torch.tensor(3.0))
    val.backward()         # compute the gradient 
    optimizer.step()

print(f.θ)

import torch
import torch.nn as nn

class LogPr(nn.Module):
   # as for Exercise 2
    
x = torch.tensor(xkcd.x, dtype=torch.float)
y = torch.tensor(xkcd.y, dtype=torch.float)
logPr = LogPr()

optimizer = torch.optim.Adam(logPr.parameters())

for epoch in range(10000):
    optimizer.zero_grad()
    loglik = logPr(y, x)
    (-loglik).backward() # we want to maximize logPr, i.e. minimize -loglik
    optimizer.step()

print(logPr(y,x))
# expected output: tensor(-61.5762, grad_fn=<SumBackward0>)

Step 4. Nested modules

To keep ourselves (reasonably) sane, it can be useful to split a Module into building blocks. If we define a module \(A\), then define another module \(B\) which uses it, as in the code below, then when we optimize over \(B\)’s unknown parameters it will automatically include \(A\)’s unknown parameters in the optimization.

class A(nn.Module):
    ...

class B(nn.Module):
    def __init__(self):
        self.a = A()

class QuadraticCurve(nn.Module):
    def forward(self, x):
        # return a + b*x + c*x^2, where x is a tensor of real values

class RQuadratic(nn.Module):
    def __init__(self):
        self.μ = QuadraticCurve()
    def logPr(self, y, x):
        # return the log likelihood of [y0,...,yn]

import torch
import torch.nn as nn

class QuadraticCurve(nn.Module):
    def __init__(self):
        super().__init__()
        self.a = nn.Parameter(torch.tensor(1.0))
        self.b = nn.Parameter(torch.tensor(1.0))
        self.c = nn.Parameter(torch.tensor(0.0))
    def forward(self, x):
        return self.a + self.b * x + self.c * x**2
    
class RQuadratic(nn.Module):
    def __init__(self):
        super().__init__()
        self.μ = QuadraticCurve()
        self.σ = nn.Parameter(torch.tensor(1.0))
    def logPr(self, y, x):
        σ2 = self.σ ** 2
        return torch.sum(- 0.5*torch.log(2*np.pi*σ2) - torch.pow(y - self.μ(x), 2) / (2*σ2))

x,y = torch.tensor(xkcd.x, dtype=torch.float), torch.tensor(xkcd.y, dtype=torch.float)
mymodel = RQuadratic()
optimizer = torch.optim.Adam(mymodel.parameters())

for epoch in range(10000):
    optimizer.zero_grad()
    loglik = mymodel.logPr(y, x)
    (-loglik).backward()
    optimizer.step()

print(loglik)
# Should give same answer as before, tensor(-61.5762, grad_fn=<SumBackward0>)

Step 5. Getting answers out of PyTorch

The magic of PyTorch is that it remembers all the mathematical operations you’ve performed and stores them in a computation graph, in order to be able to compute the derivative. When we just want to pull some values out of PyTorch for plotting, we need to tell to ignore all this cleverness.

f = MyFunction()

# Extract a scalar value, and get a Python object
f.θ.item()

# Extract a tensor, and get a numpy array
y = f(torch.tensor([1.0,2.0]))
y.detach().numpy()

# Tell it not to bother storing the computation graph
# (saves time, if we're not going to need the derivative)
with torch.no_grad():
    x = torch.tensor([1.0, 2.0])
    y = f(x)

xnew = torch.linspace(0,10,100)
with torch.no_grad():
    ynew = logPr.μ(xnew)
xnew = xnew.detach().numpy()
ynew = ynew.detach().numpy()
σhat = logPr.σ.item()

fig,ax = plt.subplots(figsize=(4,3))
ax.scatter(xkcd.x, xkcd.y)
ax.plot(xnew, ynew, color='black')
ax.fill_between(xnew, ynew-2*σhat, ynew+2*σhat, color='steelblue', alpha=.6)
plt.show()

Step 6. Making it interactive

When we optimize a function using gradient descent, how many iterations should we use? It’s hard to know, when we’re just starting out with a new model and we have no experience, and we’re still experimenting. I like to run my optimizations interactively, in an infinite loop, showing the fit every few iterations. Every so often I interrupt, explore the plots in more detail, then resume.

I’ve written a piece of magic Python code to help with this, a class called Interruptable. Use it as follows. In Jupyter, we can interrupt the while loop using the menu option Kernel | Interrupt, or by the keyboard shortcut Esc I I. We can resume by rerunning the cell with Interruptable().... (Put it in a cell on its own, so we don’t reset the epoch counter when we resume.)

import IPython
epoch = 0

with Interruptable() as check_interrupted:
    while True:
        check_interrupted()
        ... # do some stuff
        if epoch % 200 == 0:
            IPython.display.clear_output(wait=True)
            ... # print output
        epoch += 1

This code also uses IPython.display.clear_output(wait=True), to make Jupyter overwrite its output rather than appending.

x = torch.tensor(xkcd.x, dtype=torch.float)
y = torch.tensor(xkcd.y, dtype=torch.float)
mymodel = RQuadratic()  # defined in Exercise 5
epoch = 0

optimizer = torch.optim.Adam(mymodel.parameters())

def plot_quadratic(mymodel):
    with torch.no_grad():
        xnew = torch.linspace(0,10,100)
        ynew = mymodel.μ(xnew)
        xnew = xnew.detach().numpy()
        ynew = ynew.detach().numpy()
        σ = mymodel.σ.item()
    fig,ax = plt.subplots()
    ax.fill_between(xnew, ynew-2*σ, ynew+2*σ, color='steelblue', alpha=.6)
    ax.plot(xnew, ynew, color='steelblue')
    ax.scatter(x, y, color='black', marker='+', alpha=.8)
    plt.show()

with Interruptable() as check_interrupted:
    while True:
        check_interrupted()
        optimizer.zero_grad()
        loglik = torch.sum(mymodel.logPr(y, x))
        (-loglik).backward()
        optimizer.step()
        epoch += 1

        if epoch % 200 == 0:
            IPython.display.clear_output(wait=True)
            print(f'epoch={epoch} loglik={loglik.item():.4} σ={mymodel.σ:.4}')
            plot_quadratic(mymodel)

STEP 7. Using a neural network

A neural network is just another function! We can swap out the \(\mu(x)=a+bx+c x^2\) function and replace it by a neural network, i.e. a sequence of linear maps and nonlinear element-wise operations.

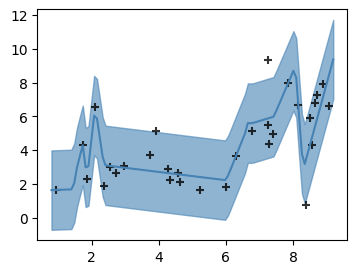
Here’s what a simple neural network looks like in PyTorch:

import torch.nn as nn

class RWiggle(nn.Module):
    def __init__(self):
        self.μ = nn.Sequential(
            nn.Linear(1,4),
            nn.LeakyReLU(),
            nn.Linear(4,20),
            nn.LeakyReLU(),
            nn.Linear(20,20),
            nn.LeakyReLU(),
            nn.Linear(20,1)
        )

• torch.nn has a built-in module nn.Linear(d,e) for multiplying by a \(d\times e\) matrix (i.e. it implements the function \(f(x)=Ax\)). All of the entries of the matrix are unknown parameters. They’re initialized randomly, and initial guesses affect the outcome of numerical optimization, thus every time we create a new RWiggle instance and fit it we’re likely to end up with a different fitted model.
• It also has a built-in module nn.LeakyReLU() which accepts any tensor as its input, and applies a simple non-linear function to each element.
• It also has a module nn.Sequential(f1,f2,...,fn) which applies a sequence of modules in turn. It saves our having to write out x1=f1(x); x2=f2(x1); ...; return xn.

One thing to watch out for: these standard building blocks are all intended to be used in a vectorized way. So nn.Linear(d,e) is actually implemented as a function \(f:\mathbb{R}^{n\times d}\to \mathbb{R}^{n\times e}\). It expects its input to be a matrix, whose rows correspond to datapoints, and it applies the linear map \(\mathbb{R}^d\to\mathbb{R}^e\) separately to each row.

When you’re getting used to PyTorch, it’s a good idea to build up your code interactively, calling x.shape on any tensor x you create, so you can double-check its size. For example,

x = torch.tensor(xkcd.x, dtype=torch.float)
print(x.shape)
xm = x[:,None]
print(xm.shape)
y = nn.Linear(1,4)(xm)
print(y.shape)

class RWiggle(nn.Module):
    def __init__(self):
        super().__init__()
        # self.μ maps R^(n×1) to R^(n×1)
        self.μ = nn.Sequential(
            nn.Linear(1,4),
            nn.LeakyReLU(),
            nn.Linear(4,20),
            nn.LeakyReLU(),
            nn.Linear(20,20),
            nn.LeakyReLU(),
            nn.Linear(20,1)
        )
        self.σ = nn.Parameter(torch.tensor(1.0))
    def logPr(self, y, x):
        # x and y are tensors of shape (n,)
        # Reshape x to be (n,1), apply μ, then drop the last dimension
        m = self.μ(x[:,None])[:,0]  
        σ2 = self.σ ** 2
        return torch.sum(- 0.5*torch.log(2*np.pi*σ2) - torch.pow(y - m, 2) / (2*σ2))

def plot_wiggle(mymodel):
    with torch.no_grad():
        xnew = torch.linspace(0,10,100)[:,None] # array dim 100×1
        ynew = mymodel.μ(xnew)                  # array dim 100×1
        xnew = xnew.detach().numpy()[:,0]       # vector length 100
        ynew = ynew.detach().numpy()[:,0]       # vector length 100
        σ = mymodel.σ.item()
    fig,ax = plt.subplots()
    ax.fill_between(xnew, ynew-2*σ, ynew+2*σ, color='steelblue', alpha=.6)
    ax.plot(xnew, ynew, color='steelblue')
    ax.scatter(x, y, color='black', marker='+', alpha=.8)
    plt.show()

x = torch.tensor(xkcd.x, dtype=torch.float)
y = torch.tensor(xkcd.y, dtype=torch.float)
mymodel = RWiggle()
epoch = 0
optimizer = torch.optim.Adam(mymodel.parameters())

with Interruptable() as check_interrupted:
    while True:
        check_interrupted()
        optimizer.zero_grad()
        loglik = mymodel.logPr(y, x)
        (-loglik).backward()
        optimizer.step()
        epoch += 1    
        if epoch % 200 == 0:
            IPython.display.clear_output(wait=True)
            print(f'epoch={epoch} loglik={loglik.item():.4} σ={mymodel.σ:.4}')
            plot_wiggle(mymodel)

STEP 8. Batched gradient descent

For large datasets, it’s not helpful to compute the full log likelihood of the entire dataset each iteration. It’s better to split the dataset up into batches, shuffle the batches, and then for each batch in turn compute the log likelihood and take a gradient-descent step. It’s better because it injects some randomness into the gradient descent process, and this helps to avoid getting stuck at local optima.

In neural network terminology, we use the word ‘epoch’ to mean ‘a pass through the entire dataset’.

PyTorch has a handy utility called DataLoader for taking an iterable object and splitting it into batches. If we give it a matrix, it splits it into groups of rows.

import torch
data = torch.tensor(np.column_stack([xkcd.x, xkcd.y]), dtype=torch.float)
data_batched = torch.utils.data.DataLoader(data, batch_size=5, shuffle=True)

data = torch.tensor(np.column_stack([xkcd.x, xkcd.y]), dtype=torch.float)
data_batched = torch.utils.data.DataLoader(data, batch_size=5, shuffle=True)

mymodel = RWiggle() # from exercise 7
optimizer = torch.optim.Adam(mymodel.parameters())
epoch = 0

with Interruptable() as check_interrupted:
    while True:
        check_interrupted()
        for b in data_batched:
            optimizer.zero_grad()
            loglik = torch.sum(mymodel.logPr(b[:,1,None], b[:,0,None]))
            (-loglik).backward()
            optimizer.step()
        epoch = epoch + 1

        if epoch % 200 == 0:
            IPython.display.clear_output(wait=True)
            print(f'epoch={epoch} loglik={loglik.item():.4} σ={σ:.4}')
            plot_wiggle(mymodel) # from exercise 6

STEP 9. Challenge

Now try it yourself!

The pytorch challenge gives you a dataset consisting of \((x,y)\) pairs, where \(x\in[0,1]\) and \(y\in\mathbb{R}^2\), and asks you to learn a smooth line through these \(y\) points by fitting the model \[ \begin{bmatrix} Y_{1}\\Y_{2} \end{bmatrix} \sim \mu(x) + \begin{bmatrix} N(0,\sigma^2)\\N(0,\sigma^2) \end{bmatrix} \]