Introduction to Functional Programming

Russ Ross

Computer Laboratory
University of Cambridge
Lent Term 2005

Lecture 8

Arrays

Conventional arrays offer indexed storage that can be updated in place

A[k] := x
inherently imperative

Purely functional languages do not have arrays implemented as a contiguous block of memory locations.

A functional array is a mapping from a finite range of integers, with lookup and update functions

lookup : 'a array -> int -> 'a
update : 'a array -> int -> 'a -> 'a array

update returns a new array, which is the same as the old array except for the value at the given index.

Arrays as binary trees

We can implement an array as a binary tree. The binary digits of the subscript dictate the path down the tree

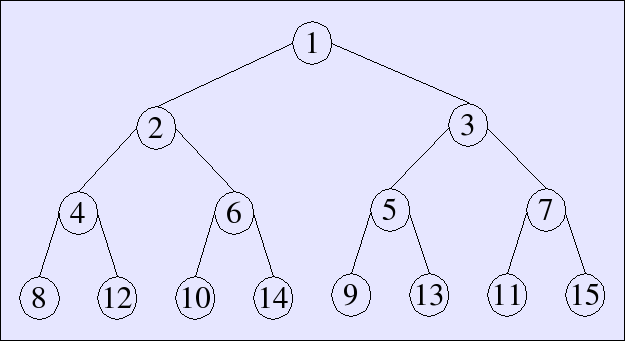
Array lookup

lookup uses the least-significant bit at each step to decide whether to go left or right.

- fun lookup Lf _ = raise Array
    | lookup (Br(elt, l, r)) i =
        if i = 1 then elt
        else if i mod 2 = 0
          then lookup l (i div 2)
          else lookup r (i div 2);
> val 'a lookup = fn : 'a tree -> int -> 'a

Array update

update is similar, but it copies everything on the way down. It can also create a new branch, but only if no branches were already created in the ancestral path. This is sufficient provided there are no gaps in the subscripting

- fun update Lf 1 v = Br (v, Lf, Lf)
    | update Lf _ _ = raise Array
    | update (Br (_, l, r)) 1 v = Br (v, l, r)
    | update (Br (elt, l, r)) i v =
        if i mod 2 = 0
          then Br (elt, update l (i div 2) v, r)
          else Br (elt, l, update r (i div 2) v);
> val 'a update = fn : 'a tree -> int -> 'a -> 'a tree

Binary numbers

Consider a representation of binary numbers as a list of digits, with the least-significant bit first

- datatype digit = Zero | One;

We can write increment and decrement functions that carry and borrow as needed

- fun inc [] = [One]
    | inc (Zero :: rest) = One :: rest
    | inc (One :: rest) = Zero :: inc rest;
> val inc = fn : digit list -> digit list

- fun dec [One] = []
    | dec (One :: rest) = Zero :: rest
    | dec (Zero :: rest) = One :: dec rest;
> val dec = fn : digit list -> digit list

Sparse binary numbers

Another way to represent binary numbers is to skip zeros and only store ones. This requires marking each one, possibly with a weight.

Our representation can now be an int list. Carry and borrow operations work based on the weights

- fun carry w [] = [w]
    | carry w (ws as w' :: ws') =
        if w < w' then w :: ws else carry (2*w) ws';
> val carry = fn : int -> int list -> int list

- fun borrow w (ws as w' :: ws') =
        if w = w' then ws' else w :: borrow (2*w) ws;
> val borrow = fn : int -> int list -> int list

Sparse binary numbers

Increment and decrement operations are just special cases of carry and borrow

- val inc = carry 1;
> val inc = fn : int list -> int list

- val dec = borrow 1;
> val dec = fn : int list -> int list

Skew binary numbers

The increment and decrement operations on binary numbers can ripple all the way through the number, taking O(log n) steps.

We can do better by changing the way we represent numbers. Instead of the weight of each digit at position n being 2ⁿ, we set it to (2ⁿ⁺¹-1).

We further change our system to allow the digits 0, 1, and 2, but stipulate that a 2 is only allowed as the first non-zero digit.

In this representation, the decimal number 92 could be written 002101 (least-significant digit first).

This system yields a single, canonical representation for every natural number.

Skew binary numbers

Observe that

2·(2ⁿ⁺¹-1) + 1 = (2ⁿ⁺²-1)

In other words, adding a 1 to a 2 yields a 1 in the next position.

We can increment a skew binary number that contains a two by resetting the two to zero and incrementing the next digit from zero to one, or from one to two (the second digit cannot be two).

To increment a skew binary number that doesn't contain a two, increment the lowest digit from zero to one or one to two. The result will still be in canonical form.

Note that there are no rippling carry operations. If we use a sparse representation, increment and decrement operations run in constant time.

Skew binary numbers

The positions in skew binary numbers have weights:

1, 3, 7, 15, 31, 63, 127, 255, 1023, 2047, …

Counting looks like this (again with least-significant digit first):

1, 2, 01, 11, 21, 02, 001, 101, 201, 011, 111, 211, 021, 002, 0001, 1001, 2001, 0101, 1101, 2101, 0201, …

Skew binary numbers

The code is simpler than the description. We represent numbers as a list of integer weights. The same weight repeated indicates a two

- fun inc (ws as w1 :: w2 :: rest) =
        if w1 = w2 then (1 + w1 + w2) :: rest else 1 :: ws
    | inc ws = 1 :: ws;
> val inc = fn : int list -> int list

- fun dec (1 :: ws) = ws
    | dec (w :: ws) = (w div 2) :: (w div 2) :: ws;
> val dec = fn : int list -> int list

With this representation, counting looks like:

[1], [1,1], [3], [1,3], [1,1,3], [3,3], [7], [1,7], [1,1,7], [3,7], [1,3,7], [1,1,3,7], [3,3,7], [7,7], [15], …

Random-access lists

Normal lists have O(1) cons, head, and tail operations, but looking up an element by subscript n takes n operations. With a data structure based on skew binary numbers, we can retain O(1) complexity for list operations, and permit lookup and update operations by subscript with O(log n) complexity.

The idea is to have a skew binary list, where each position holds a binary tree with as many elements as the weight of that position.

Example

Here is how a skew binary random-access list would look with 13 elements, i.e., 021 or [3, 3, 7]:

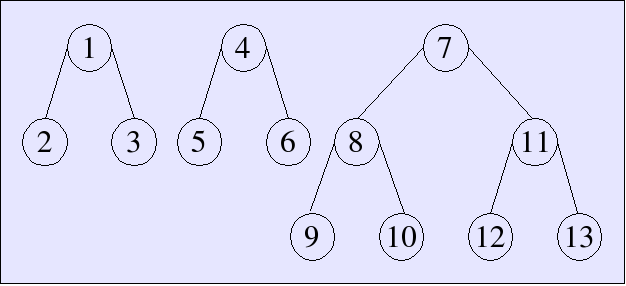
Example

Here is how a skew binary random-access list would look with 17 elements, i.e., 2001 or [1, 1, 15]:

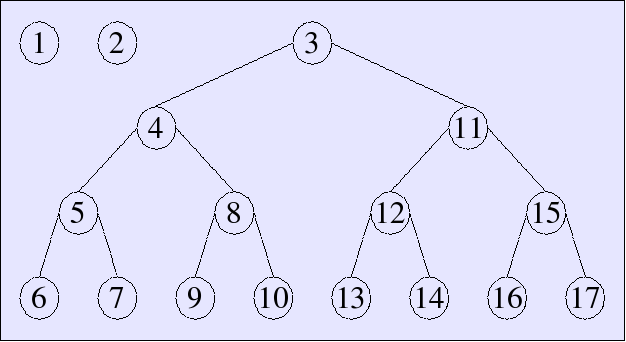
Datatype

We use a datatype for the trees. Each tree is a complete preorder binary tree with the following datatype

- datatype 'a tree = Lf of 'a | Br of 'a * 'a tree * 'a tree;

The skew binary random-access list is just a list of (weight, tree) pairs, where each tree is a complete binary tree with weight elements, and the weights follow the rules outlined earlier for skew binary numbers.

Cons, head, and tail

The cons, head, and tail operations are patterned after inc and dec

fun cons (x, ts as (w1, t1) :: (w2, t2) :: ts') =
      if w1 = w2 then (1+w1+w2, Br(x, t1, t2)) :: ts'
      else (1, Lf x) :: ts
  | cons (x, ts) = (1, Lf x) :: ts

fun head [] = raise Empty
  | head ((1, Lf x) :: ts) = x
  | head ((w, Br(x, t1, t2)) :: ts) = x

fun tail [] = raise Empty
  | tail ((1, Lf x) :: ts) = ts
  | tail ((w, Br(x, t1, t2)) :: ts) =
      (w div 2, t1) :: (w div 2, t2) :: ts;

> val 'a cons = fn : 'a * (int * 'a tree) list ->
      (int * 'a tree) list
  val 'a head = fn : (int * 'a tree) list -> 'a
  val 'a tail = fn : (int * 'a tree) list ->
      (int * 'a tree) list

Lookup

Lookup operations have two parts: first scan the list to find the right tree, and then search the tree for the right element. Given an index, the first step is just a matter of skipping trees and subtracting their weights from the index

fun lookup (i, []) = raise Subscript
  | lookup (i, (w, t) :: ts) =
      if i < w then lookupTree (w, i, t)
      else lookup (i - w, ts);
> val 'a lookup = fn : int * (int * 'a tree) list -> 'a

Searching the tree is similar to other tree searches we've seen, but it uses the subscript to search the tree in preorder, i.e., ordered root node first, then everything to the left, the everything to the right

fun lookupTree (1, 0, Lf x) = x
  | lookupTree (1, i, Lf x) = raise Subscript
  | lookupTree (w, 0, Br(x, t1, t2)) = x
  | lookupTree (w, i, Br(x, t1, t2)) =
      if i <= w div 2 then lookupTree (w div 2, i-1, t1)
      else lookupTree (w div 2, i-1 - w div 2, t2);
> val 'a lookupTree = fn : int * int * 'a tree -> 'a

Update

Update is very similar, but it makes copies as it goes

fun updateTree (1, 0, y, Lf x) = Lf y
  | updateTree (1, i, y, Lf x) = raise Subscript
  | updateTree (w, 0, y, Br(x, t1, t2)) = Br(y, t1, t2)
  | updateTree (w, i, y, Br(x, t1, t2)) =
      if i <= w div 2
        then Br(x, updateTree (w div 2, i-1, y, t1), t2)
        else Br(x, t1, updateTree (w div 2, i-1 - w div 2, y, t2))

fun update (i, y, []) = raise Subscript
  | update (i, y, (w, t) :: ts) =
      if i < w then (w, updateTree (w, i, y, t)) :: ts
      else (w, t) :: update (i-w, y, ts);
> val 'a updateTree = fn : int * int * 'a * 'a tree -> 'a tree
  val 'a update = fn : int * 'a * (int * 'a tree) list ->
      (int * 'a tree) list

Computer Laboratory, University of Cambridge, 15 February 2005