


Next: Fourier Analysis
Up: No Title
Previous: Signals and Systems
The above system h(t) is linear if it obeys the properties of superposition
and proportionality:
- Superposition implies that if r1(t) is the system's
response to any input s1(t), and if r2(t) is the system's response
to any input s2(t), then the system's response to a third input
s3(t)=s1(t)+s2(t) which is the sum of the earlier two inputs,
must simply be the sum of its responses to those two inputs separately:
r3(t)=r1(t)+r2(t).
- Proportionality implies that if any input s(t)is changed just
by multiplying it by a constant k (which may be complex), then the
system's original response r(t) simply gets multiplied by the same
(possibly complex) constant: kr(t).
Linear systems are thus always described by some
linear operator h(t).
Examples of such linear operators are:
- Any derivative, or combination of derivatives of any order; any
linear differential operator with constant coefficients.
- An integral expression.
- A convolution with some fixed waveform.
- Any combination or concatenation of the above.
The eigenfunctions
of a system are those inputs which emerge completely
unchanged at the output, except for multiplication by a constant (which
may be complex). A fundamental property of linear systems as described
above is that their eigenfunctions are the complex exponentials
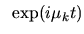 :
That is, the only effect which a linear system h(t) can have on an input
which is a complex
exponential is to multiply it by a complex constant A when
generating a response to it. Obviously, other families of input signals
would become
quite dramatically changed when operated upon by the sorts of linear operators
ennumerated above. So, complex exponentials are a very special and important
class of functions. In fact, if one can learn how a linear system h(t)
responds to all possible complex exponentials (that is to say, if one can
measure the complex constant A associated with every possible frequency
:
That is, the only effect which a linear system h(t) can have on an input
which is a complex
exponential is to multiply it by a complex constant A when
generating a response to it. Obviously, other families of input signals
would become
quite dramatically changed when operated upon by the sorts of linear operators
ennumerated above. So, complex exponentials are a very special and important
class of functions. In fact, if one can learn how a linear system h(t)
responds to all possible complex exponentials (that is to say, if one can
measure the complex constant A associated with every possible frequency
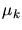 of an input complex exponential), then one has complete knowledge
about how the system will respond to any other possible input!
This is
an extraordinary kind of power.
of an input complex exponential), then one has complete knowledge
about how the system will respond to any other possible input!
This is
an extraordinary kind of power.
The process works by representing any possible input as a superposition
of complex exponentials, and then applying the superposition principles
described earlier in order to calculate the output as another linear
combination of those same complex exponentials, since they are eigenfunctions.
In order to understand and apply this, we need to develop some of the tools
of Fourier Analysis.



Next: Fourier Analysis
Up: No Title
Previous: Signals and Systems
Neil Dodgson
2000-10-23