When more than one client wants to use a resource at once we have contention.
Real queues are used in hardware, either in FIFO memories or by flow control applying backpressure on the source to stall it until the contended resource is available. An arbiter allocates a resource to one client at a time.
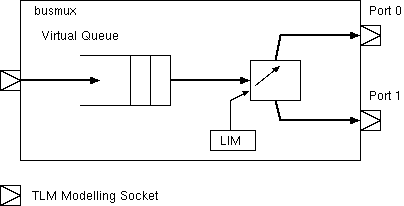
Contention like this can be modelled using real or virtual queues:
Delay estimates can be based on dynamic measurements of utilisation at the contention point, in terms of transactions per millisecond and a suitable formula, such as 1/(1-p) that models the queuing delay in terms of the utilisation.
// A simple bus demultiplexor: forwards transaction to one of two destinations:
busmux::write(u32_t A, u32_t D, sc_time &delay)
{
// Do actual work
if (A >= LIM) port1.write(A-LIM, D, delay) else port0.write(A, D, delay);
// Measure utilisation (time for the last 100 transactions)
if (++opcount == 100)
{ sc_time delta = sc_time_stamp() - last_measure_time;
local_processing_delay = delay_formula(delta, opcount); // e.g. 1 + 1/(1-p) nanoseconds
logging.log(100, delta); // record utilisation
last_measure_time = sc_time_stamp();
opcount = 0;
}
// Add estimated (virtual) queuing penalty
delay += local_processing_delay;
}

In the above, a delay formula function knows how many bus cycles per unit time can be handled and hence can compute and record the utilisation and queuing delays.
The value `p' is the utilisation in the range 0 to 1. From queuing theory, with random arrivals, the queuing delay goes to infinity following a 1/(1-p) response as p approaches unity. For uniform arrival and service times, the queuing delay goes sharply to infinity at unity.
| 26: (C) 2008-13, DJ Greaves, University of Cambridge, Computer Laboratory. |