Advanced Algorithms

Lecturer: Dr A.C. Norman (acn1@cl.cam.ac.uk)

No. of lectures + examples classes: 12 + 4

Prerequisite course: Data Structures and Algorithms

Aims

This course aims to provide a sampling of topics that are similar in style to those discussed in the Data Structures and Algorithms course, but which are of a more specialised or advanced nature. This is intended not just to give a concrete understanding of the particular methods discussed but to make students aware of something of the depth and breadth of algorithmic techniques that have been developed: a variety of techniques and results will be mentioned in passing and without full explanation or proof to try to give an impression of this.

Lectures

• Binomial and Fibonacci Heaps: these grow out of a desire to solve the single-source shortest path problem (e.g. using Dijkstra's algorithm) on sparse graphs as fast as possible. Maybe the surprise is that Dijkstra's algorithm as documented at a IB level fails to think harder about this--but there again when you see how messy Fibonacci Heaps are you will understand!

• Kolmogorov Complexity: Usually evaluations of the information content or complexity of things will be asymptotic, and arbitrary finite odd-cases will be quietly ignored. This part of the course provides some basis for considering a finite string such as ``ababababababab'' to be less complex than one like ``abbbaabaaabaaaa''. This involves looking at various ideas about data compression, Turing machines, probabilities and information theory. Note very well that I will only give a simple introduction to a large and difficult subject area.

• Probabilistic Algorithms: The relationship between true randomness and computer-generated pseudo-random numbers. The extent to which a truly random ``oracle'' might be a help in algorithm design, including a discussion of the fact that there are several different ways of producing precise models of what ``successful random computation'' might mean. One of the most important areas where probabilistic algorithms are commonplace: integer primality checking and factorisation. While I intend to duck most technical issues this borders on including a bit of computational number theory.

• More Garbage Collection: The background challenge here will be to take a procedure which is easily implemented as one that takes place in large disruptive chunks and to derive schemes that support (near-) real-time processing. I may discuss both ``ephemeral'' garbage collection and the issues behind true parallel garbage collection where one processor continuously allocates and uses memory while another rushes along in the background tidying up. Note that the widespread adoption of Java has made Garbage Collection a hotter topic than it had seemed for a while!

• High Precision Arithmetic. In late 1999 the record for computing the value of 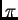$\pi$ was 206,158,430,000 decimal digits. [just think about the disc space needed to store this, let alone calculate it!]. At precisions well less than this non-classical algorithms for arithmetic and the calculation of elementary functions and constants become important and I will discuss some of them. Big numbers also arise in many computer algebra applications and often rather different techniques (based on residue class arithmetic) are required to render computations feasible.

Objectives

On completing the course, students should

• understand and be able to both describe and apply the particular techniques that were covered in detail

• be able to recognise and comment coherently on different models for evaluating algorithms (e.g. practical versus theoretical efficiency, various forms of probabilistic measures of reliability, provably optimal methods)

• appreciate that the range of techniques that have been developed is very large, and that many of the algorithms are far from obvious or easy to understand

Recommended books

Knuth, D.E. (1998). The Art of Computer Programming, vol. II. Addison-Wesley (3rd ed.).
Cormen, T.H., Leiserson, C.E. & Rivest, R.L. (1990). Introduction to Algorithms. McGraw-Hill.

Those wanting yet greater depth and completeness are referred to the Handbook of Theoretical Computer Science, Volume A edited by van Leeuwen (1990) and during the course a number of references into the primary literature will be provided.