


Next: Digital Electronics
Up: Michaelmas Term 2001: Part
Previous: Continuous Mathematics
Contents
Data Structures and Algorithms
Lecturer: Dr M. Richards
(mr@cl.cam.ac.uk)
No. of lectures: 16
This course is a prerequisite for Computer Graphics & Image
Processing, Complexity Theory and Advanced Algorithms (Part II).
Aims
The aim of this course is to provide a comprehensive introduction
to computer algorithms taken from many different areas of application.
The course will concentrate on algorithms that are of fundamental
importance and the efficiency of most of them will be analysed.
Lectures
- Fundamentals.
Models of a computer, costs, growth rates.
- Simple data structures.
Arrays, lists, trees. Idea of abstract data type.
- Ideas for algorithm design.
Divide and Conquer and other important styles of algorithm.
- The TABLE data type.
Multiple implementation models for a single ADT, including hash
tables.
- Free storage management.
Reference counts and garbage collection.
- Sorting.
Insertion, Shell, Quick, Heap, Tree, Merge and Radix.
Selection of
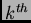 element in
element in 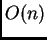 .
.
- Storage on external media.
Larsen's method, B-trees.
- Variants on the SET data type.
Balanced, 2-3-4, red-black, splay and ternary trees.
- String searching.
Brute force, Knuth-Morris-Pratt, Boyer-Moore, Rabin-Karp algorithms.
- Data compression.
Run length encoding, prediction, Move-to-Front, Huffman, arithmetic
encoding, Lempel-Ziv, and Wheeler's Block Compression.
- Algorithms on graphs.
Reachability and shortest paths. Warshall, Floyd, Dijkstra, Prim and
Kruskal algorithms. Depth first and breadth first traversal, strongly
connected components. Matchings in bi-partite graphs.
- Geometric algorithms.
Inside-outside a closed figure? Do line segments cross? Convex
hull.
Objectives
At the end of the course students should
- have a good understanding of how several fundamental
algorithms work, particularly those concerned with sorting
and table look up
- be able to analyse the efficiency in terms of space and
time of most algorithms
- be familiar with several techniques used in data compression and
algorithms on graphs
- be able to design new algorithms or modify existing ones for new
applications and reason about the efficiency of the result
Recommended books
Sedgewick, R. (1990). Algorithms in C. Addison-Wesley.
Cormen, T.H., Leiserson, C.D. & Rivest, R.L. (1990). Introduction to
Algorithms. MIT Press.
Manber, U. (1989). Introduction to Algorithms: A Creative Approach.
Addison-Wesley.
Salomon, D. (1998). Data Compression: The Complete Reference.
Springer.



Next: Digital Electronics
Up: Michaelmas Term 2001: Part
Previous: Continuous Mathematics
Contents
Christine Northeast
Tue Sep 4 09:34:31 BST 2001