Discrete Mathematics

Lecturer: Dr P. Robinson (pr@cl.cam.ac.uk)

No. of lectures: 16 (Continued into Lent Term)

This course is a prerequisite for Introduction to Security (Part IB), Information Theory and Coding (Part II) and Security (Part II).

Aims

This course will develop the idea of formal proof by way of examples involving simple objects such as integers and sets. The material enables academic study of Computer Science and will be promoted with examples from the analysis of algorithms and cryptography.

Lectures

Part A. Integers

• Proof. Deduction, contradiction. Integers, mathematical induction. [2 lectures]

• Factors. Division: highest common factors and least common multiples. Euclid's algorithm: solution in integers of ax+by=c, the complexity of Euclid's algorithm. Euclid's proof of the infinity of primes. Existence and uniqueness of prime factorisation. Irrationality of 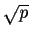$\sqrt{p}$; brief discussion of rational and algebraic numbers. [3 lectures]

• Modular arithmetic. Solving congruences. Units modulo m, Euler's totient function. Wilson's theorem. Chinese remainder theorem. The Fermat-Euler theorems. Public key cryptography. [3 lectures]

Part B. Sets, functions and relations.

• Sets, subsets and Boolean operations. Indicator (characteristic) functions and their algebra. Principle of inclusion-exclusion, with applications to Euler's function. Boolean logic. [2 lectures]

• Binary relations. Composition of relations. Equivalence relations and quotients of sets. Closures and Warshall's algorithm. Partial orders and total orders. Hasse diagrams. Well-founded relations and well ordering. Structural induction. [3 lectures]

• Functions. Injective, surjective and bijective functions. Numbers of such functions between sets. Sorting. The Schröder-Bernstein theorem. Countability. A countable union of countable sets is countable. The uncountability of R. Existence of transcendental numbers. [3 lectures]

Objectives

On completing the course, students should be able to

• write a clear statement of a problem as a theorem in mathematical notation; prove and disprove assertions using a variety of techniques

• describe, analyse and use Euclid's algorithm; explain and apply prime factorisation
• perform calculations with modular arithmetic; use number theory to explain public key cryptography

• analyse problems using set theory; explain and use the principle of inclusion and exclusion

• recognise relations and discuss their properties; describe and analyse Warshall's algorithm

• state, prove and apply the Schröder-Bernstein theorem; distinguish countable and uncountable sets

Recommended books

Biggs, N.L. (1989). Discrete Mathematics. Oxford University Press.
Conway, J.H. & Guy, R.K. (1996). The Book of Numbers. Springer-Verlag.
Davenport, H. (1992). The Higher Arithmetic. Cambridge University Press (6th ed.).
Giblin, P. (1993). Primes and Programming. Cambridge University Press.
Graham, R.L., Knuth, D.E. & Patashnik, O. (1994). Concrete Mathematics. Addison-Wesley (2nd ed.).
Humphreys, J.F. & Prest, M.Y. (1989). Numbers, Groups and Codes. Cambridge University Press.
Mattson, H.F. Jr (1993). Discrete Mathematics. Wiley.
Nissanke, N. (1999). Introductory Logic and Sets for Computer Scientists. Addison-Wesley.
Pólya, G. (1980). How to Solve It. Penguin.
Rosen, K.H. (1999). Discrete Mathematics and its Applications. McGraw-Hill (4th ed.).